A metallic ball has spherical cavity at its centre. If the ball is heated, what happens to the cavity
Its volume decreases.
Its volume remains constant.
Its volume increases.
Nothing can be decided.
The correct Answer is:C
To solve the question about what happens to a spherical cavity at the center of a metallic ball when the ball is heated, we can follow these steps:
1. Understanding the Structure:
- We have a metallic ball with a spherical cavity at its center. Let's denote the radius of the metallic ball as R and the radius of the cavity as r.
2. Effect of Heating:
- When the metallic ball is heated, the entire material of the ball expands due to thermal expansion. This is a property of metals where they tend to increase in volume when their temperature rises.
3. Volume Expansion:
- The volume expansion of the metallic ball can be described by the formula:
V=V0(1+γΔT)
where V0 is the initial volume, γ is the coefficient of volume expansion, and ΔT is the change in temperature.
4. Calculating Initial Volume:
- The initial volume of the metallic ball (excluding the cavity) can be expressed as:
V0=43πR3−43πr3=43π(R3−r3)
5. Volume Increase:
- As the temperature increases, the volume V of the metallic ball will increase. Since the volume of the ball is directly related to its radius (specifically, the radius cubed), both the radius of the metallic ball and the radius of the cavity will increase.
6. Conclusion:
- Therefore, when the metallic ball is heated, both the metallic material surrounding the cavity and the cavity itself will expand. This means that the radius of the cavity will increase as well.
Final Answer:
When the metallic ball is heated, the cavity at its center also expands, resulting in an increase in the radius of the cavity.
---
- We have a metallic ball with a spherical cavity at its center. Let's denote the radius of the metallic ball as R and the radius of the cavity as r.
- When the metallic ball is heated, the entire material of the ball expands due to thermal expansion. This is a property of metals where they tend to increase in volume when their temperature rises.
- The volume expansion of the metallic ball can be described by the formula:
V=V0(1+γΔT)
where V0 is the initial volume, γ is the coefficient of volume expansion, and ΔT is the change in temperature.
- The initial volume of the metallic ball (excluding the cavity) can be expressed as:
V0=43πR3−43πr3=43π(R3−r3)
- As the temperature increases, the volume V of the metallic ball will increase. Since the volume of the ball is directly related to its radius (specifically, the radius cubed), both the radius of the metallic ball and the radius of the cavity will increase.
- Therefore, when the metallic ball is heated, both the metallic material surrounding the cavity and the cavity itself will expand. This means that the radius of the cavity will increase as well.
When the metallic ball is heated, the cavity at its center also expands, resulting in an increase in the radius of the cavity.
Topper's Solved these Questions
- MISCELLANEOUS QUESTIONSBook:MCGROW HILL PUBLICATIONChapter:MISCELLANEOUS QUESTIONSExercise:PART-B
Explore 99 Videos
- MEASUREMENTBook:MCGROW HILL PUBLICATIONChapter:MEASUREMENTExercise:ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
Explore 13 Videos
- MOTIONBook:MCGROW HILL PUBLICATIONChapter:MOTIONExercise:HIGHER ORDER THINKING QUESTIONS
Explore 48 Videos
Similar Questions
A uniformly charged hemisphere of radius b and charge density ρ has a hemispherical cavity of radius a(a=b2) cut from its centre. If the potential at the centre of the cavity is nρb216ε0 then n=?

View SolutionA solid spherical conductor of radius R has a spherical cavity inside it (see figure). A point charge q is placed at the centre of the cavity. (a) What is the potential of the conductor? (b) If the charge q is shifted inside the cavity by a distance Δx, how does the potential of the conductor change? (c) How does your answer to the question (a) and (b) change if the cavity is not spherical and the charge q is placed at any point inside it (see figure) (d) Draw electric field lines in entire space in each case. In which case all field lines are straight lines
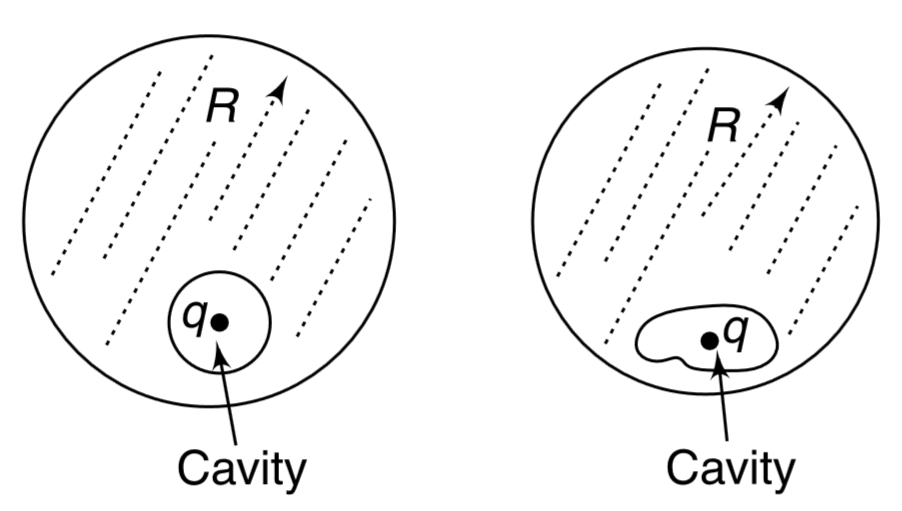
View Solution
Knowledge Check
A solid metal ball has a spherical cavity. If the ball is heatd, the volume of the cavity will
AincreaseBdecreaseCremain unffecetedDremain unaffected but the sphere of the cavity will changeA solid ball of metal has a concentric spherical cavity within it. If the ball is heated, the volume of the cavity will
AIncreaseBDecreaseCRemain sameDAll of theseA solid metal ball has aspherical cavity .If the ball is heated ,the volume of the vavity will
AincreaseBdecreaseCremain unaffectedDNone of these
A spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed
View SolutionA spherical metallic conductor has a spherical cavity. A positive charge is placed inside the cavity at its centre. Another positive charge is placed outside it. The conductor is initially electrically neutral.
Column I (Cause)Column II (Effect)(A)If outside is shifted to other position(p)Distribution of charge on innner surfaceof cavity charges(B)If inside charge is shifted to other position(q)Distribution of charge on outer surface ofconductor charges(C)If magnitude of charge inside cavity is(r)Electric potential at the centre of conductorincreasedchanges due to charges presenton outer surface of conductor(D)If conductor is earthed(s)Force on the charge placed insidecavity changes
View SolutionA metallic sphere of diameter D has a cavity of diameter d at its centre. If the sphere is heated, the diameter of the cavity will:
View SolutionA solid ball of metal has a spherical cavity inside it. The ball is cooled. The volume of the cavity will
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
View Solution

