A plane mirror reflecting a ray of incident light is rotated through an angle of 30∘ about an axis through the point of incidence in the plane of the mirror and perpendicular to the plane of incidence then
the incident ray is fixed
the reflected ray rotates through an angle θ
the reflected ray rotates through an angle θ/2
the reflected ray rotates through an angle of 2θ
The correct Answer is:D
To solve the problem of how much the reflected ray rotates when a plane mirror is rotated through an angle of 30∘, we can follow these steps:
1. Understand the Setup:
- We have a plane mirror and an incident ray of light striking the mirror.
- The mirror is rotated through an angle of 30∘ about an axis that is perpendicular to the plane of incidence.
2. Identify the Angle of Rotation:
- The angle through which the mirror is rotated is given as 30∘. This is denoted as ω=30∘.
3. Determine the Effect on the Reflected Ray:
- According to the laws of reflection, when a plane mirror is rotated, the angle of the reflected ray changes. Specifically, the change in the angle of the reflected ray is twice the angle through which the mirror is rotated.
- Therefore, if the mirror rotates by ω, the reflected ray will rotate by 2ω.
4. Calculate the Total Rotation of the Reflected Ray:
- Since ω=30∘, the rotation of the reflected ray will be:
Rotation of reflected ray=2×ω=2×30∘=60∘
5. Conclusion:
- The reflected ray will rotate through an angle of 60∘ when the plane mirror is rotated through an angle of 30∘.
Final Answer:
The reflected ray rotates through an angle of 60∘.
---
- We have a plane mirror and an incident ray of light striking the mirror.
- The mirror is rotated through an angle of 30∘ about an axis that is perpendicular to the plane of incidence.
- The angle through which the mirror is rotated is given as 30∘. This is denoted as ω=30∘.
- According to the laws of reflection, when a plane mirror is rotated, the angle of the reflected ray changes. Specifically, the change in the angle of the reflected ray is twice the angle through which the mirror is rotated.
- Therefore, if the mirror rotates by ω, the reflected ray will rotate by 2ω.
- Since ω=30∘, the rotation of the reflected ray will be:
Rotation of reflected ray=2×ω=2×30∘=60∘
- The reflected ray will rotate through an angle of 60∘ when the plane mirror is rotated through an angle of 30∘.
The reflected ray rotates through an angle of 60∘.
Topper's Solved these Questions
- REFLECTION OF LIGHT Book:MCGROW HILL PUBLICATIONChapter:REFLECTION OF LIGHT Exercise:HIGHER ORDER THINKING QUESTIONS
Explore 10 Videos
- MOTIONBook:MCGROW HILL PUBLICATIONChapter:MOTIONExercise:HIGHER ORDER THINKING QUESTIONS
Explore 48 Videos
- REFRACTION OF LIGHTBook:MCGROW HILL PUBLICATIONChapter:REFRACTION OF LIGHTExercise:HIGHER ORDER THINKING QUESTIONS
Explore 37 Videos
Similar Questions
A plane mirror reflecting a ray of incident light is rotated through an angle q about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
(1) The reflected ray rotates through an angle 2q
(2) The incident ray is fixed
(3) The reflected ray does not rotate
(4) The reflected ray rotates through an angle q
View SolutionFor a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
View Solution
Knowledge Check
A plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotateBThe reflected ray rotates through an angle θCThe reflected ray rotates through an angle 2θDThe incident ray is fixedA plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotate.BThe reflected ray rotates through an angle θ.CThe reflected ray rotates through an angle 2θ.DNone of theseA plane mirror reflects a beam of light to from a real image. The incident beam is
AparallelBconvergentCdivergentDany one of the above
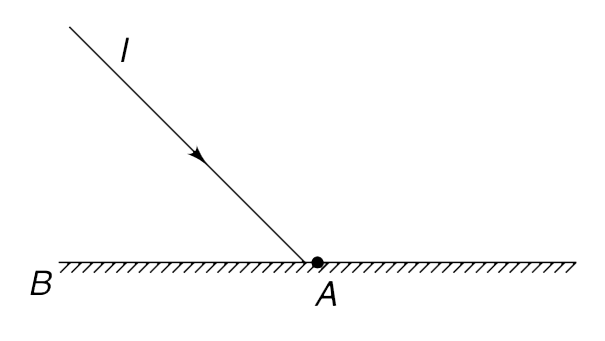
I is a ray incident on a plane mirror. Keeping the incident ray fixed, the mirror is rotated by an angle θ about an axis passing through A perpendicular to the plane of the Fig. show that the refracted ray rotates through an angle 2θ. Does your answer differ if the mirror is rotated about an axis passing through B?
View SolutionA ray of light is incident on a plane mirror placed horizontally. When the mirror is rotated through an angle 30∘ the reflected ray is found to be directed along the vertical. Determine the angle of incidence at the initial position of the mirror.
View SolutionIf a light ray incident on a plane mirror makes an angle 30∘ with it, find the angle of incidence and angle of reflection.
View SolutionIf a ray of light incident on a plane mirror is such that it makes an angle of 30∘ with the mirror, then the angle of reflection is
View SolutionA ray of light is incident on a plane mirror at an angle of 20∘ with the normal, at the point of incidence, Through what angle, the ray of light will be deviated from its direction of incidence ?
View Solution

