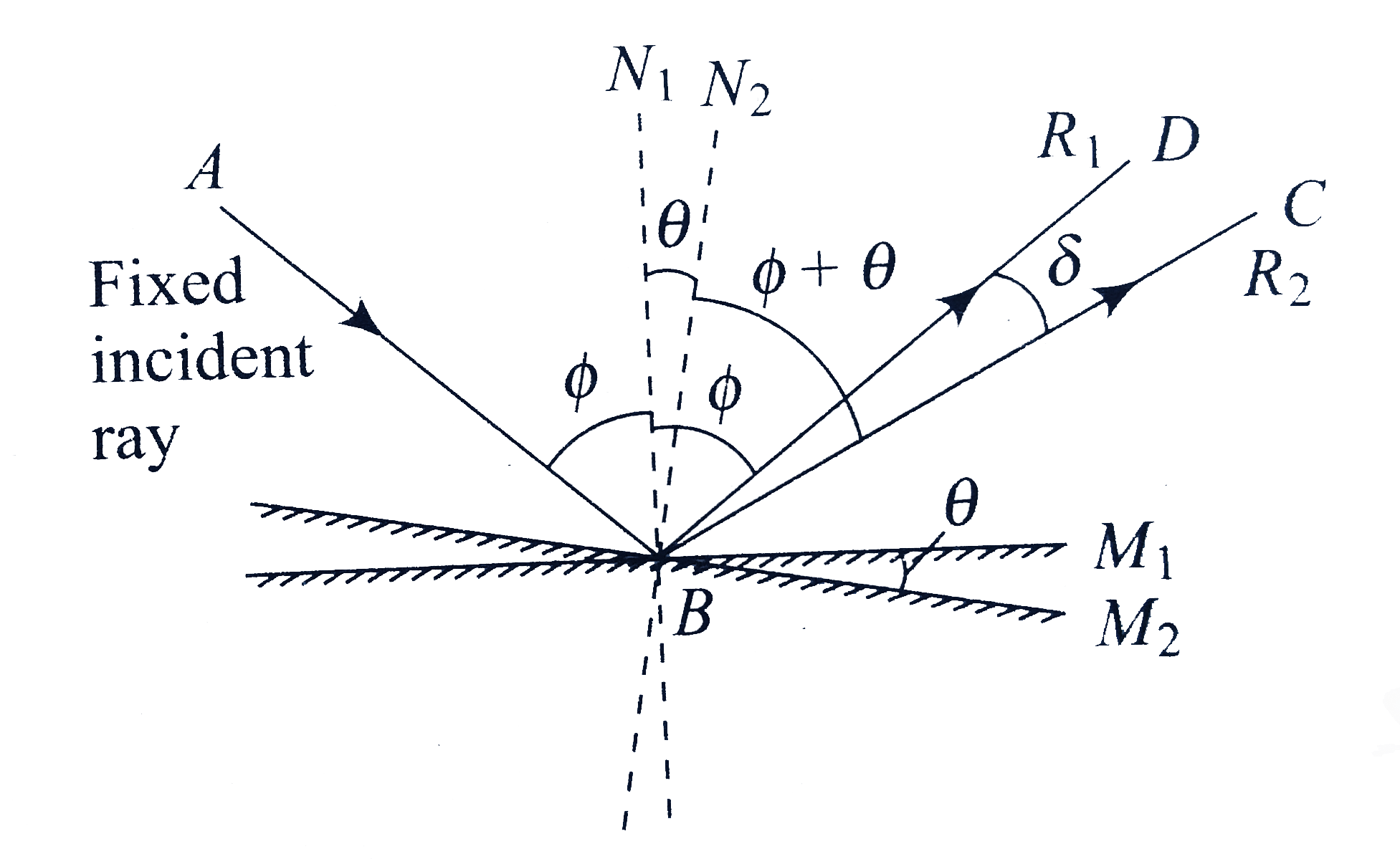
For a fixed incident light ray, if the mirror be rotated through and angle θ (about an axis which lies in the plane of mirror and perpendicular to the plane of incidence), show that the reflected ray turns through an angle 2θ in same sense.
In Fig. , M1,N1,and R1 indicate the initial position of mirror, normal, and direction of reflected light ray, respectively, M2,N2, and R2 indicate the final position of mirror, normal, and direction of reflected light ray, respectively.
If the mirror is rotated by and angle θ, new angle of incidence
=∠ABN2=ϕ+θ
Angle of deviation of final ray =∠DBC=δ
∠DBC=∠ABC−∠ABD=2(ϕ+θ)−2ϕ=2θ
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
A plane mirror reflecting a ray of incident light is rotated through an angle q about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
(1) The reflected ray rotates through an angle 2q
(2) The incident ray is fixed
(3) The reflected ray does not rotate
(4) The reflected ray rotates through an angle q
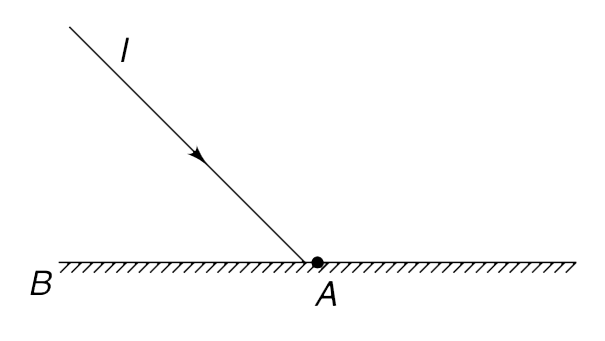
View SolutionI is a ray incident on a plane mirror. Keeping the incident ray fixed, the mirror is rotated by an angle θ about an axis passing through A perpendicular to the plane of the Fig. show that the refracted ray rotates through an angle 2θ. Does your answer differ if the mirror is rotated about an axis passing through B?
View Solution
Knowledge Check
A plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotateBThe reflected ray rotates through an angle θCThe reflected ray rotates through an angle 2θDThe incident ray is fixedA plane mirror, reflecting a ray of incident light, is rotated through an angle θ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotate.BThe reflected ray rotates through an angle θ.CThe reflected ray rotates through an angle 2θ.DNone of theseA plane mirror reflecting a ray of incident light is rotated through an angle of 30∘ about an axis through the point of incidence in the plane of the mirror and perpendicular to the plane of incidence then
Athe incident ray is fixedBthe reflected ray rotates through an angle θCthe reflected ray rotates through an angle θ/2Dthe reflected ray rotates through an angle of 2θ
For a given incident ray, when a plane mirror is turned……….. The reflected ray turns through………. .
View SolutionShow that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionBy what angle the mirror must be rotated such that the reflected ray becomes vertical. Let the light ray incident on the plane mirror with an angle of incidence theta with respect to horizontal
View SolutionWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
View SolutionWhen mirror is rotated through an angle θ, a reflected ray from it moves through an angle of
View Solution

