The relation between T and g is given by
T∝g
T∝g2
T2∝g
T∝√1g
The correct Answer is:D
To find the relation between the time period T of a simple pendulum and the acceleration due to gravity g, we can follow these steps:
1. Understanding the Pendulum: A simple pendulum consists of a mass (bob) attached to a string or rod of fixed length L. When the pendulum swings, it undergoes oscillatory motion.
2. Defining Time Period: The time period T is defined as the time taken for the pendulum to complete one full oscillation, which includes moving from the mean position to the extreme position and back.
3. Formula for Time Period: The formula for the time period of a simple pendulum is given by:
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
4. Analyzing the Relation: From the formula, we can see that:
- T is proportional to the square root of the length L and inversely proportional to the square root of g.
- This means that if g increases, T decreases, and vice versa.
5. Expressing the Inverse Relationship: We can express the relationship between T and g as:
T∝1√g
This indicates that the time period T is inversely proportional to the square root of the acceleration due to gravity g.
6. Alternative Form: If we square both sides of the equation, we can also express it as:
T2∝1g
This shows that the square of the time period T2 is directly proportional to the inverse of g.
7. Conclusion: Therefore, the relation between the time period T and the acceleration due to gravity g can be summarized as:
- T∝1√g or T2∝1g.
Final Answer:
The relation between T and g is given by:
- T∝1√g (or equivalently, T2∝1g).
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
- T is proportional to the square root of the length L and inversely proportional to the square root of g.
- This means that if g increases, T decreases, and vice versa.
T∝1√g
This indicates that the time period T is inversely proportional to the square root of the acceleration due to gravity g.
T2∝1g
This shows that the square of the time period T2 is directly proportional to the inverse of g.
- T∝1√g or T2∝1g.
The relation between T and g is given by:
- T∝1√g (or equivalently, T2∝1g).
Topper's Solved these Questions
- WAVE MOTION AND SOUND BOOK - MCGROW HILL PUBLICATIONCHAPTER - WAVE MOTION AND SOUND EXERCISE - HIGH ORDER THINKING QUESTIONS
22 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
- WORK AND ENERGYBOOK - MCGROW HILL PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING QUESTIONS
29 Videos
Similar Questions
Knowledge Check
For an adiabatic process the relation between V and T is given by
ATVγ= constantBTγV=constantCTV1−γ= constantDTVγ−1=constantAccording to Einstein, the relation between mass and energy is given by
AE=mc2Bm=Ec2CE=mc−2DE=mc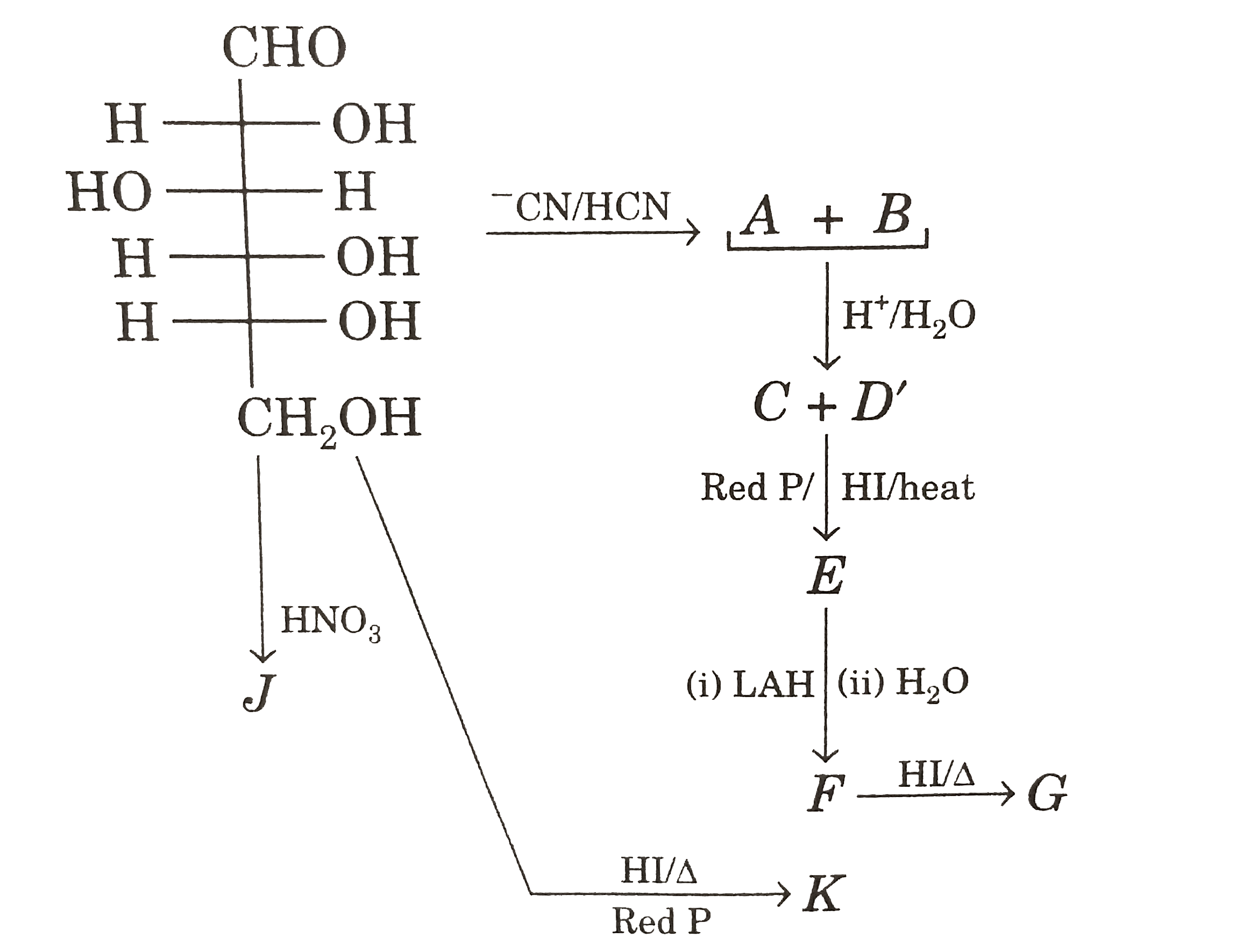
What is relation between G and K?AChain isomerBpositional isomerCHomologueDNone of these
The relation between time t and distance x for a moving body is given as t=mx2+nx, where m and n are constants. The retardation of the motion is : (When v stands for velocity)
View SolutionSelect the pair which has the same relation between the words as the relation between the words of given pair. Horse : gallop
View SolutionThe distance of point of a compound pendulum form its centre of gravity is l, the time period of oscillation relative to this point T. If g=π2, the relation between l and T will be :-
View SolutionThe relation between time t and distance x is t=ax2+bx where aandb are constants. The acceleration is
View SolutionA Centigreade scales A and B have triple points of water defined to be 200A and 300B (given triple point of water is =276.16K). The relation between TA and TB is
View Solution