The distance of point of a compound pendulum form its centre of gravity is l, the time period of oscillation relative to this point T. If g=π2, the relation between l and T will be :-
l2−[T24]l+k2=0
l2+[T24]l+k2=0
l2−[T24]l−k2=0
l2+[T24]l−k2=0
The correct Answer is:A
_E01_028_S01.png)
τ=−mgsinθl⇒lα=−mglsinθ
⇒m=−glθ(l2+k2)=−ω2θ(sin~θ)
⇒α=−glθ(l2+k2)=−ω2θ⇒ω=√gll+k2
⇒T=2πω=2π√l2+k2gl=2√l2+k2l[g=π2]
⇒l2−(T24)l+k2=0
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-02
Explore 19 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise- 3 Match The Column
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Knowledge Check
In a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
AL/T=ConstantBL2/T2= ConstantCL/T2=ConstantDLT=ConstantFor a bar pendulum the distance between two points of minimum time period is
Aequal to the radius of gyrationBtwice the radius of gyrationCtwice the length of an equivalent simple pendulumDtwice the length fo a compound pendulumThe period of oscillation of a simple pendulum of constant length at surface of the earth is T. Its time period inside mine will be
AIncreasesBDecreasesCNo changeDNone
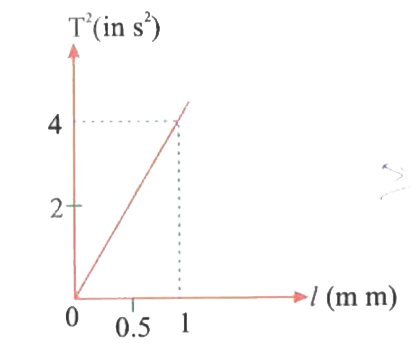
The l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
View SolutionA simple pendulum oscillates in air with time period T and amplitude A . As the time passes
View SolutionThe distance between the point of suspension and the centre of gravity of a compound pendulum is l and the radius of gyration about the horizontal axis through the centre of gravity is k, then its time period will be
View SolutionIf the time period of a simple pendulum is T=2π√l/g , then the fractional error in acceleration due to gravity is
View SolutionHow does time period (T) of a seconds pendulum vary with length(l)?
View Solution
