A ray of light when falls on a liquid A-air interface at angle 45∘, it just gets total reflection. When a ray of light falls on liquid B -air interface at angle 30∘, it does not emerge out. We can infer that
μA>μB
μA<μB
μA=μB
can't be inferred
The correct Answer is:B
To solve the problem, we need to analyze the conditions for total internal reflection and the critical angles for the two liquids involved (liquid A and liquid B).
1. Understanding Total Internal Reflection (TIR):
- Total internal reflection occurs when light travels from a denser medium to a rarer medium and the angle of incidence exceeds the critical angle (θc).
- The critical angle can be calculated using the formula:
θc=sin−1(n2n1)
where n1 is the refractive index of the denser medium and n2 is the refractive index of the rarer medium (in this case, air).
2. Analyzing Liquid A:
- Given that light falls on the liquid A-air interface at an angle of 45∘ and experiences total internal reflection, we can conclude that:
θAc=45∘
- Using the critical angle formula:
sin(45∘)=nairnA⟹nA=nairsin(45∘)=nair1√2=nair⋅√2
3. Analyzing Liquid B:
- For liquid B, light falls on the liquid B-air interface at an angle of 30∘ and does not emerge, which means that the critical angle for liquid B must be equal to or less than 30∘:
θBc≤30∘
- Using the critical angle formula again:
sin(30∘)=nairnB⟹nB=nairsin(30∘)=nair12=2⋅nair
4. Comparing Refractive Indices:
- From the calculations:
- nA=nair⋅√2
- nB=2⋅nair
- To compare nA and nB:
nA<nB⟹nair⋅√2<2⋅nair
- Dividing both sides by nair (assuming nair>0):
√2<2
- This inequality holds true.
5. Conclusion:
- From the above analysis, we conclude that the refractive index of liquid A is less than that of liquid B:
nA<nB
Final Answer:
We can infer that the refractive index of liquid A is less than that of liquid B.
- Total internal reflection occurs when light travels from a denser medium to a rarer medium and the angle of incidence exceeds the critical angle (θc).
- The critical angle can be calculated using the formula:
θc=sin−1(n2n1)
where n1 is the refractive index of the denser medium and n2 is the refractive index of the rarer medium (in this case, air).
- Given that light falls on the liquid A-air interface at an angle of 45∘ and experiences total internal reflection, we can conclude that:
θAc=45∘
- Using the critical angle formula:
sin(45∘)=nairnA⟹nA=nairsin(45∘)=nair1√2=nair⋅√2
- For liquid B, light falls on the liquid B-air interface at an angle of 30∘ and does not emerge, which means that the critical angle for liquid B must be equal to or less than 30∘:
θBc≤30∘
- Using the critical angle formula again:
sin(30∘)=nairnB⟹nB=nairsin(30∘)=nair12=2⋅nair
- From the calculations:
- nA=nair⋅√2
- nB=2⋅nair
- To compare nA and nB:
nA<nB⟹nair⋅√2<2⋅nair
- Dividing both sides by nair (assuming nair>0):
√2<2
- This inequality holds true.
- From the above analysis, we conclude that the refractive index of liquid A is less than that of liquid B:
nA<nB
We can infer that the refractive index of liquid A is less than that of liquid B.
Topper's Solved these Questions
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:AIPMT/NEET
Explore 55 Videos
- OPTICSBook:MTG GUIDEChapter:OPTICSExercise:Topicwise Practice Questions
Explore 200 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:AIPMT/NEET (MCQs)
Explore 48 Videos
Similar Questions
Knowledge Check
When a ray of light emerges from a block of glass, the critical angle is
Aequal to the angle of reflectionBthe angle between the reflected ray and the normalCthe angle of incidence for which the refracted ray traveles along the glass air boundaryDthe angle of incidenceWhen a ray of light emerges from a block of glass, the critical angle is
AEqual to the angle of reflectionBThe angle between the refracted ray and the normalCThe angle of incidence for which the refracted ray travels along the glass-air boundaryDThe angle of incidenceA ray of light is incident at the glass-water interface at an angle i, it emerges finally parallel to the surface of water, then the value of pg would be
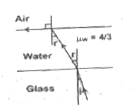 A(43) sin(i)B[1sin(i)]C43D1
A(43) sin(i)B[1sin(i)]C43D1
A ray of light falls on a mirror normally. What are the values of angle of incedence and the angle of reflection.
View SolutionA light ray falls on the air glass interface at an angle of 30∘. What is the angle of refraction for this rays ? (nag=32).
View SolutionTotal internal reflection of a ray of light is possible when the (ic= critical angle, i= angle of incidence)
View SolutionA ray of light falls on a glass slab making an angle of 45∘ with normal. The emergent ray makes the same angle with normal. It shows that
View SolutionA ray of light travelling in air falls obliquely on the surface of a clam poun. It will
View Solution

