A ray of light falls on a mirror normally. What are the values of angle of incedence and the angle of reflection.
To solve the problem of determining the angles of incidence and reflection when a ray of light falls normally on a mirror, we can follow these steps:
1. Understand the Setup:
- We have a mirror and a ray of light that strikes the mirror. The ray is said to fall "normally," which means it is perpendicular to the surface of the mirror.
2. Define the Normal Line:
- The normal line is an imaginary line that is perpendicular to the surface of the mirror at the point of incidence.
3. Identify the Angle of Incidence:
- The angle of incidence (θ₁) is defined as the angle between the incident ray and the normal line. Since the ray falls normally, this angle is 0 degrees.
- Therefore, θ₁ = 0°.
4. Apply the Law of Reflection:
- According to the law of reflection, the angle of reflection (θ₂) is equal to the angle of incidence (θ₁). Mathematically, this can be expressed as:
θ₁ = θ₂
5. Determine the Angle of Reflection:
- Since θ₁ = 0°, it follows that θ₂ must also be 0°.
- Therefore, θ₂ = 0°.
6. Conclusion:
- The values of the angle of incidence and the angle of reflection when a ray of light falls normally on a mirror are both 0 degrees.
Final Answer:
- Angle of Incidence (θ₁) = 0°
- Angle of Reflection (θ₂) = 0°
- We have a mirror and a ray of light that strikes the mirror. The ray is said to fall "normally," which means it is perpendicular to the surface of the mirror.
- The normal line is an imaginary line that is perpendicular to the surface of the mirror at the point of incidence.
- The angle of incidence (θ₁) is defined as the angle between the incident ray and the normal line. Since the ray falls normally, this angle is 0 degrees.
- Therefore, θ₁ = 0°.
- According to the law of reflection, the angle of reflection (θ₂) is equal to the angle of incidence (θ₁). Mathematically, this can be expressed as:
θ₁ = θ₂
- Since θ₁ = 0°, it follows that θ₂ must also be 0°.
- Therefore, θ₂ = 0°.
- The values of the angle of incidence and the angle of reflection when a ray of light falls normally on a mirror are both 0 degrees.
- Angle of Incidence (θ₁) = 0°
- Angle of Reflection (θ₂) = 0°
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-263videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
A ray of light falls on a plane mirror at angle of 35∘. The value of θ is
 A35∘B45∘C55∘D90∘
A35∘B45∘C55∘D90∘ - Question 2 - Select One
A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBAC - Question 3 - Select One
A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBAC
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
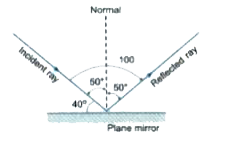
refracted rays is 90∘?View SolutionThe angle between an incident ray and the mirror is 40∘.
(i) What is the angle of incidence?
(ii) What is the angle of reflection?
(iii) What is the total angle through which the ray of light turns?
 View Solution
View SolutionTwo mirrors A and B are placed at right angles to each other as shown in Fig.16.4.
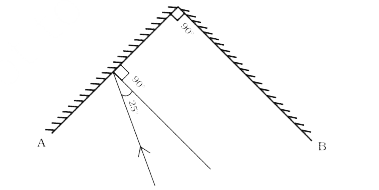
A ray of light incident on mirror A at an angle of 250 falls on mirror B after reflection. The angle of reflection for the ray reflected from mirror B would beView SolutionA ray of light is incident on a convex mirror at angle of incidence of 40∘. What is the ratio of angle of reflection to the angle of incidence?
View SolutionA ray of light is incident at an angle of 30∘ with the plane of a plane mirror. Find the angle of reflection.
View Solution


