A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
zero
4q√3πε0b
qπε0b
4qπε0b
The correct Answer is:B
All the eight charges are symmetrically situated at the eight vertices of the cube, each at a distance r equal to half the longest diagonal from the centre.
Length of the longest diagonal of the cube,
d=√(b2+b2+b2)=√3b Hence, r=d2=√32b
Potential at the centre of the cube due to all the eight charges is,
V=8×14πε0qr=8×14πε0×q√32b=4q√3πε0b
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS
1 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS
18 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- ELECTRONIC DEVICESBOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)
42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
A cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
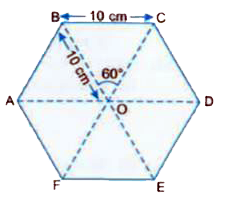
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
View Solution
Knowledge Check
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A0B14π∈0.qa2C14π∈0.6qa2D14π∈0.6q2a2A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104VA cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
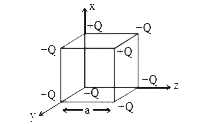 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionA cube of side a has a charge q at each of its vertices. The potential energy of the system, of charges is "(Kq^(2))/(a)((12)/(z)+6sqrt(x)+(4)/(sqrt(y)))." Then find "x+y+z".
View SolutionGiven a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View SolutionThe total electric flux through a cube when a charge 8q is placed at one corner of the cube is
View Solution
