Given that for a reaction of nth order the integrated rate equation is
K=1t(n−1)[1Cn−1−1Cn−10] where C and C0 are the concentration of reactant at time to initiallyh respectivley. The t3/4 and t1/2 are related as (t3/4 is time required to C to become C/4)Solution in Telugu
t3/4=t1/2[2n−1+1]
t3/4=t1/2[2n−1−1]
t3/4=t1/2[2n+1+1]
t3/4=t1/2[2n+1−1]
The correct Answer is:A
(t34)(t12)=[2(n−1)+1]
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-II LINKED COMPREHENSION TYPE QUESTIONS)
9 Videos
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-III MATCH THE FOLLOWING QUESTIONS)
3 Videos
- CHEMICAL KINETICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-1 (EXERCISE -II ORDER, MOLECULARITY, HALF LIFE:)
34 Videos
- CHEMICAL KINETCSBOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETCSEXERCISE - EXERCISE - 3.2
45 Videos
- CHEMICAL THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - Additional Practice Exercise
54 Videos
Similar Questions
A certain endothermic reaction: A→ Product, ΔH=+ve proceeds ina sequence of three elementary steps with the rate constant K1,K2 and K3 and each one having energy of activation E1,E2 and E3 respectively at 25∘C. The observed rate constannt for the reaction is equal to K3√K1K2.
A1,A2 and A3 are Arrhenius parameters respectively.
The observed energy of activation for the reaction is
View SolutionMatch the following columns
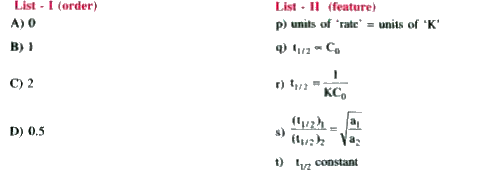
View SolutionSucrose decompose in acid solution into glucose and fructose according to the first order rate law, with t12=3.00 hours. What fraction of sample of sucrose remains after 8 hours ?
View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
View SolutionWhich among the following is not an exact differential?
View SolutionIf tn=14(n+2)(n+3) for n=1,2,3,.... then 1t1+1t2+1t3+....+1t2003=
View SolutionThe order of reaction is an experimentally determined quanity. It may be zero, poistive, negative, or fractional. The kinetic equation of nth order reaction is
k×t=1(n−1)[1(a−x)n−1−1an−1] …(i)
Half life of nth order reaction depends on the initial concentration according to the following relation:
t1/2∝1an−1 ...(ii)
The unit of the rate constant varies with the order but general relation for the unit of nth order reaction is
Units of k=[1Conc]n−1×Time−1 ...(iii)
The differential rate law for nth order reaction may be given as:
dXdt=k[A]n ...(iv)
where A denotes the reactant.
The rate constant for zero order reaction is
where c0 and ct are concentration of reactants at respective times.
View SolutionGiven that for a reaction of nth order, the integrated rate equation is:
K=1t(n−1)[1Cn−1−1Cn−10], where C and C0 are the concentration of reactant at time t and initially respectively. The t3/4 and t1/2 are related as t3/4 is time required for C to become C1/4) :
View SolutionShow that the time t_(1//2)//t_(3//4) for n^(th) order reaction is a function of 'n' alone. t_(3//4) is the time required for concentration to become 1//4 of original concentration.
View SolutionGiven that for a reaction of order n. the intergrated form of the rate equation is k= (1)/(t(n-1))[(1)/(C^(n-1))-(1)/(C_(0)^(n-1))] where C_(0) and C are the values after time t. What is the relationship between t_(3//4) and t_(1//2) where t_(3//4) is the time required for C to become 1//4C_(0)-
View SolutionA certain reaction obeys the rate equation (in the integrated form) [C^(1-n)-C_(@)^(1-n)]=(n-1) kt where C_@ is the initial concentration of C is the concentration after time, t Then:
View Solutionसिद्ध कीजिए कि (i) C1−2C2+3C3−4C4+...+n(−1)n−1Cn=0
(ii) a−(a−1)C1+(a−2)C2−(a−3)C3+...+(−1)n(a−n)Cn=0
(iii) aC0−(a+d)C1+(a+2d)C2−(a+3d)C3+...+(−1)n(a+nd)Cn=0
(iv) C0−22C1+32C2−42C3+...+(−1)n(n+1)2Cn=0,n>0
View Solutionसिद्ध कीजिए कि -
(i) (C0+C1)(C1+C2)(C2+C3)(C3+C4)...(Cn−1+Cn)=C0C1C2...Cn−1(n+1)nn!
(ii) C1C0+2C2C1+3C3C2+...+nCnCn−1=n(n+1)2
(iii) C20+C21+C22+...+C2n=(2n)!(n!)2=1⋅3⋅5...(2n−1)n!2n
(iv) C0C1+C1C2+C2C3+...+Cn−1Cn=(2n)!(n−1)!(n+1)!=1⋅3⋅5...(2n−1)(n+1)!n⋅2n
(v) C0Cr+C1Cr+1+C2Cr+2+...+Cn−rCn=(2n)!(n−r)!(n+r)!
View Solutionसिद्ध कीजिए कि -
(i) C0+C12+C23+...+Cnn+1=2n+1−1n+1
(ii) C0−C12+C23−C34+...+(−1)nCnn+1=1n+1
View SolutionGiven that for a reaction of order n, the integrated from of the rate equation is :
k=1t(n−)[10Cn−1−1Cn−10] where C0 and C are the values of the reactant concentration at the start and after tme t. What is the relationship between t3/4 and t1/2 where t3/4 is the time required for C to become 14C0?
View Solution
