Question

A wire of length L and cross section area A is kept on a horizontal surface and one of its end is fixed at point 0. A ball of mass m is tied to its other end and the system is rotated with angular velocity $\omega .$ Show that increase in its length. $\Delta l=\frac{m{\omega }^2{L}^2}{AY}.Y$ is young’s modulus.

Explanation

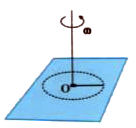
By rotating the ball of mass m with angular speed w, the pseudo centifugal force acting on it due to centripetal force
`F = ( mv ^(2))/( ) = ( mL ^(2) omega ^(2))/( L )`
`F = mL iomega^(2)`
`therefore` ongitudinal stress `sigma = (F)/(A) = (mL omega ^(2))/(A) `
Let increase in length of rod `= Dela L`
`therefore` strain `= (Delta L )/(L)`
Young modulus `Y = ("stress")/("strain") = ( m Lomega ^(2))/(A) //(Delta L )/(L)`
`therefore Delta L = (m L ^(2) omega ^(2))/(A.Y)`