(A): ABAB ..... pattern of close packing gives hcp arrangement
(R): In hcp arrangement each sphere is associated with two tetrahedral voids Solution in Telugu
Both (A) and (R) are true. (R) properly explain (A)
Both (A) and (R) are true. (R) does not explain (A)
(A) is true. (R) is false
(A) is false. (R) is true
The correct Answer is:B
Step by step video, text & image solution for (A): ABAB ..... pattern of close packing gives hcp arrangement (R): In hcp arrangement each sphere is associated with two tetrahedral voids by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLIDS STATEBook:AAKASH SERIESChapter:SOLIDS STATEExercise:OBJECTIVE EXERCISE - 2 (PROPERTIES OF SOLIDS)
Explore 11 Videos
- SOLID STATEBook:AAKASH SERIESChapter:SOLID STATEExercise:PRACTICE SHEET - 5
Explore 30 Videos
- SOLUTIONS Book:AAKASH SERIESChapter:SOLUTIONS Exercise:Objective Exercise -4
Explore 50 Videos
Similar Questions
To get n-type semiconductor, impurity to be added to silicon should have the following number of valence electrons
View SolutionThe closest-packing sequence ABAB....... represents
View SolutionAssertion : Molarity of a solution decreases with an increase of temperature
Reason : As temperature increases volume of the solution increases.
View SolutionIf in a closest packed arrangement r is the radius of the sphere respresenting the tetrahedral void and R is the radius of the spheres in closest packed arrangement then
View SolutionWhat are tetrahedral and octahedral voids in a close-packed structure of particles? How many voids are there in a ccp structure of 'N' atoms? Why is the number of octahedral voids in an hcp or a ccp arrangement of particles equal to the number of packed particles?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
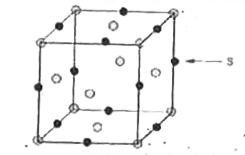
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionThe arrangement of spheres in hexagonal close packing (hcp) is :
View SolutionTotal number of tetrahedral and octahedral voids in hcp arrangment are 1218.
View SolutionAssertion (A) : Packing efficiency of hcp and ccp structures is 74%.
Reason (R) : If the number of close packed spheres is N, then number of tetrahedral voids is N.
View Solution(A): ABAB ..... pattern of close packing gives hcp arrangement
(R): In hcp arrangement each sphere is associated with two tetrahedral voids
View SolutionWhat is the number of octahedral voids per sphere in hcp arrangement?
View SolutionWhat is the number of terahedral voids per sphere in hcp arrangement?
View Solution

