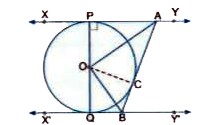
XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
In quad. APQB, we have
∠APO=90∘ and ∠BQO=90∘ [∵ tangent at any point is perpendicular to the radius through the point of contact].
Now, ∠APO+∠BQO+∠QBC+∠PAC=360∘
⇒∠PAC+∠QBC=360∘−(∠APO+∠BQO)=180∘……(i)
We have
∠CAO=12∠PAC and ∠CBO=12∠QBC [∵tangents from an external point are equally inclined to the line segment joining the centre to that point].
∴∠CAO+∠CBO=12(∠PAC+∠QBC)=12×180∘=90∘.........(ii)
In ΔAOB, we have
∠CAO+∠AOB+∠CBO=180∘
⇒∠AOB=180∘−(∠CAO+∠CBO)=90∘ [using (i)]
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8A
Explore 16 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8B
Explore 15 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
Similar Questions
In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View Solution
Knowledge Check
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘AB and AC are tangents to the circle with centre O. Then x equals.
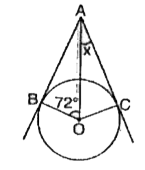 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘
landm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
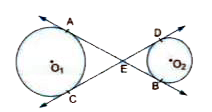
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
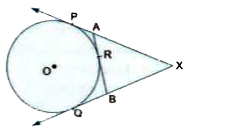
View SolutionIn Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View SolutionAB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the ∠BDOis
View Solution
