Let P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that
ar(||gm PQRS)=12ar(quad. ABCD).
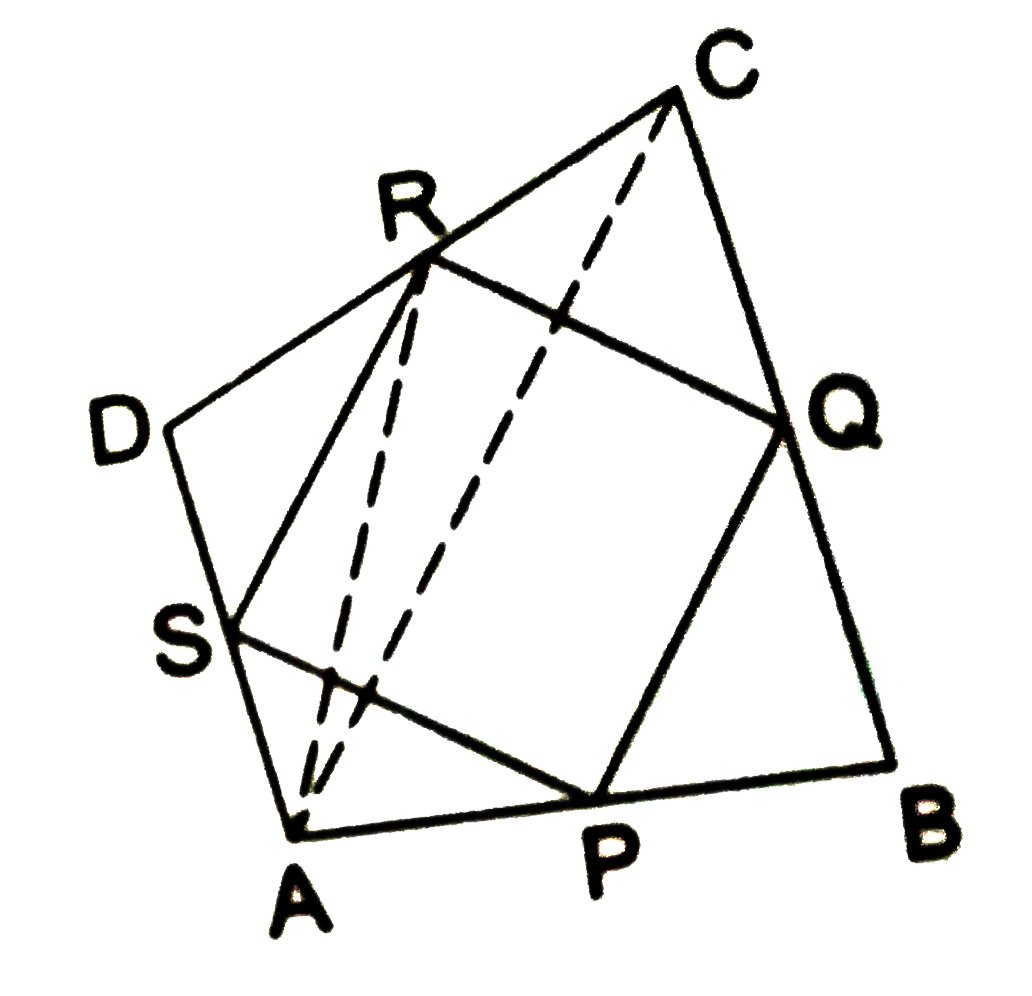
Join AC and AR.
In △ABC, P and Q are midpoints of AB and BC respectively.
∴ PQ||AC and PQ =12AC.
In △DAC, S and R are midpoints of AD and DC respectively.
∴ SR||AC SR=12AC.
Thus, PQ||SR and PQ = SR.
∴ PQRS is a ||gm.
Now, median AR divides △ACD into two △ of equal area.
∴ar(△ARD)=12ar(△ACD). ...(i)
Median RS divides △ARD into two △ of equal area.
∴ar(△DSR)=12ar(△ARD). ...(ii)
From (i) and (ii), we get ar(△DSR)=14ar(△ACD).
Similarly, ar(△BQP)=14ar(△ABC).
∴ar(△DSR)+ar(△BQP)=14[ar(△ACD)+ar(△ABC)]
⇒ar(△DSR)+ar(△BQP)=14ar[quad.ABCD]. ...(iii)
Similarly, ar(△CRQ)+ar(△ASP)=14ar(quad. ABCD). ...(iv)
Adding (iii) and (iv), we get
ar(△DSR)+ar(△BQP)+ar(△CRQ)+ar(△ASP)
=12ar(quad. ABCD) ...(v)
But, ar(△DSR)+ar(△BQP)+ar(△CRQ)+ar(△ASP)
+ar(||gm PQRS)=ar( .ABCD)....(vi)
Substracting (v) from (vi), we get
ar(||gm PQRS)=12ar(quad. ABCD).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
P, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
ar(|| gm PQRS)=12×ar(∣∣gmABCD).
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution
Knowledge Check
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32AC
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a quadrilateral in which AB=CD and AD=BC. show that it is a parallelogram.
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, Show that ar(EFGH)=12AR (ABCD)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View Solution
