Show that a median of a triangle divides it into two triangles of equal area.
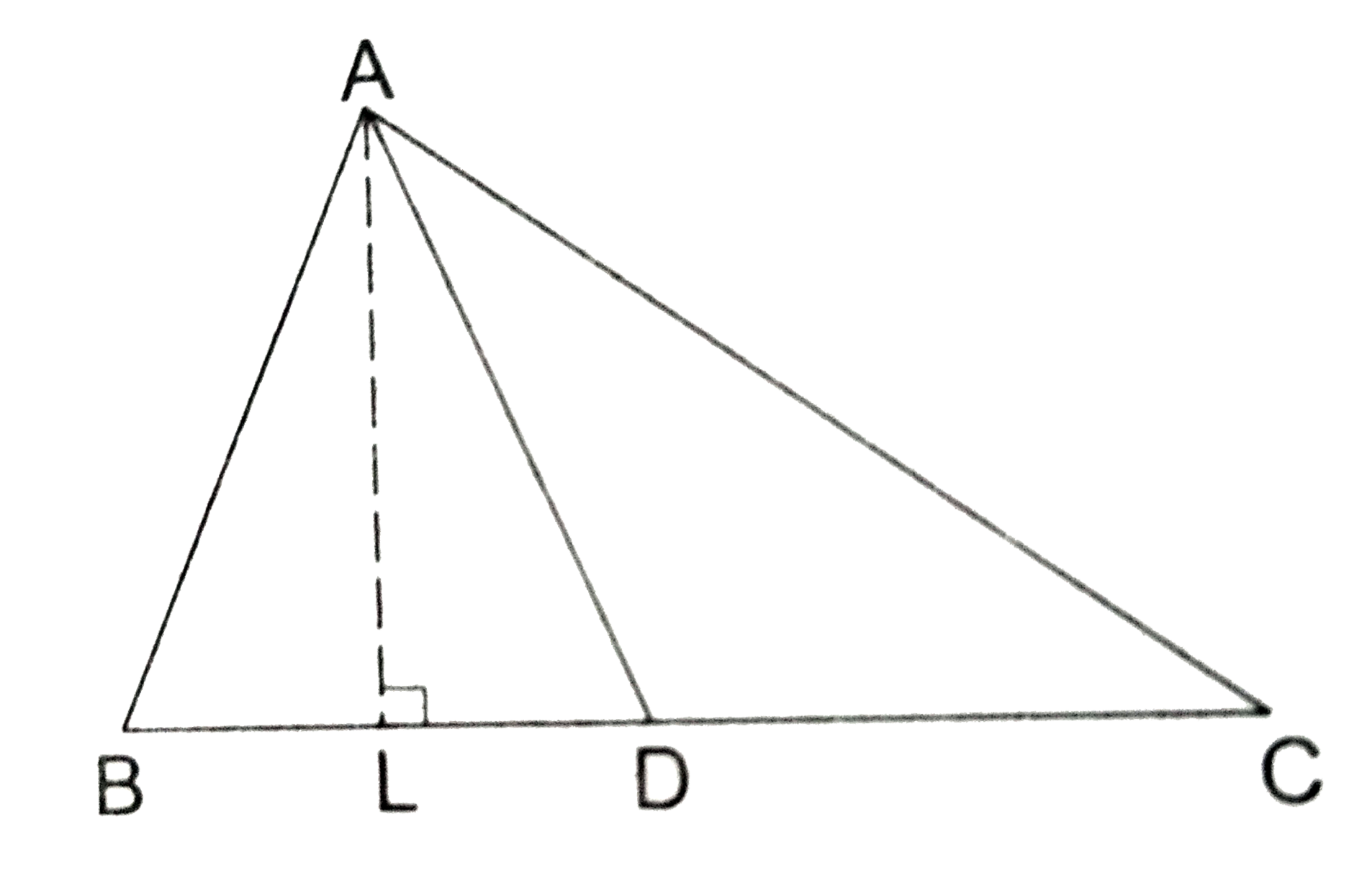
GIVEN A △ ABC in which AD is median.
TO PROVE ar(△ABD)=ar(△ADC).
CONSTRUCTION Draw AL⊥BC.
PROOF Since D is the midpoint of BC, we have
BD = DC.
Now, BD = DC
⇒12BD×AL=12DC×AL⇒ar(△ABD)=ar(△ADC).
Hence,a median of a triangle divides it into two triangle of equal area.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:Exercise 11
Explore 38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBook:RS AGGARWALChapter:AREAS OF TRIANGLES AND QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
Similar Questions
If A(4,−6),B(3,−2)andC(5,2) are the vertices of ABC, then verify the fact that a median of a triangle ABC divides it into two triangles of equal areas.
View SolutionAs we know studied that a median of a triangle divides it into triangles of equal areas. Verify this result for ΔABC whose vertices are A (4,-6), B(3,-2) and C (5,2).
View Solution
Knowledge Check
The median of a triangle divides it into two
Atriangles of equal areaBcongruent trianglesCright angled trianglesDisosceles trianglesAssertion (A) : If ABCD is a rhombus whose one angle is 60∘ then the ratio of the lengths of its diagonals is √3:1
Reason (R ) : Median of a triangle divides it into two triangle of equal area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.Consider the following statements in respect of any triangle
I. The three medians of a triangle divide it into six triangles of equal area.
II. The perimeter of a triangle is greater than the sum of the lengths of its three medians.
Which of the statements given above is/are correct ?AI onlyBII onlyCBoth I and IIDNeither I nor II
A diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionEach diagonal of a ||gm divides it into two triangles of the same area
View SolutionIf both the diagonals of a quadrilateral divides it into four triangles of equal area, then the quadrilateral is a rhombus.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionAsserion (A) : The diagonals of a ||gm divide it into four triangle of equal area.
Reason (R ) : A diagonal of a ||gm divides it into two triangle of equal area.
View Solution