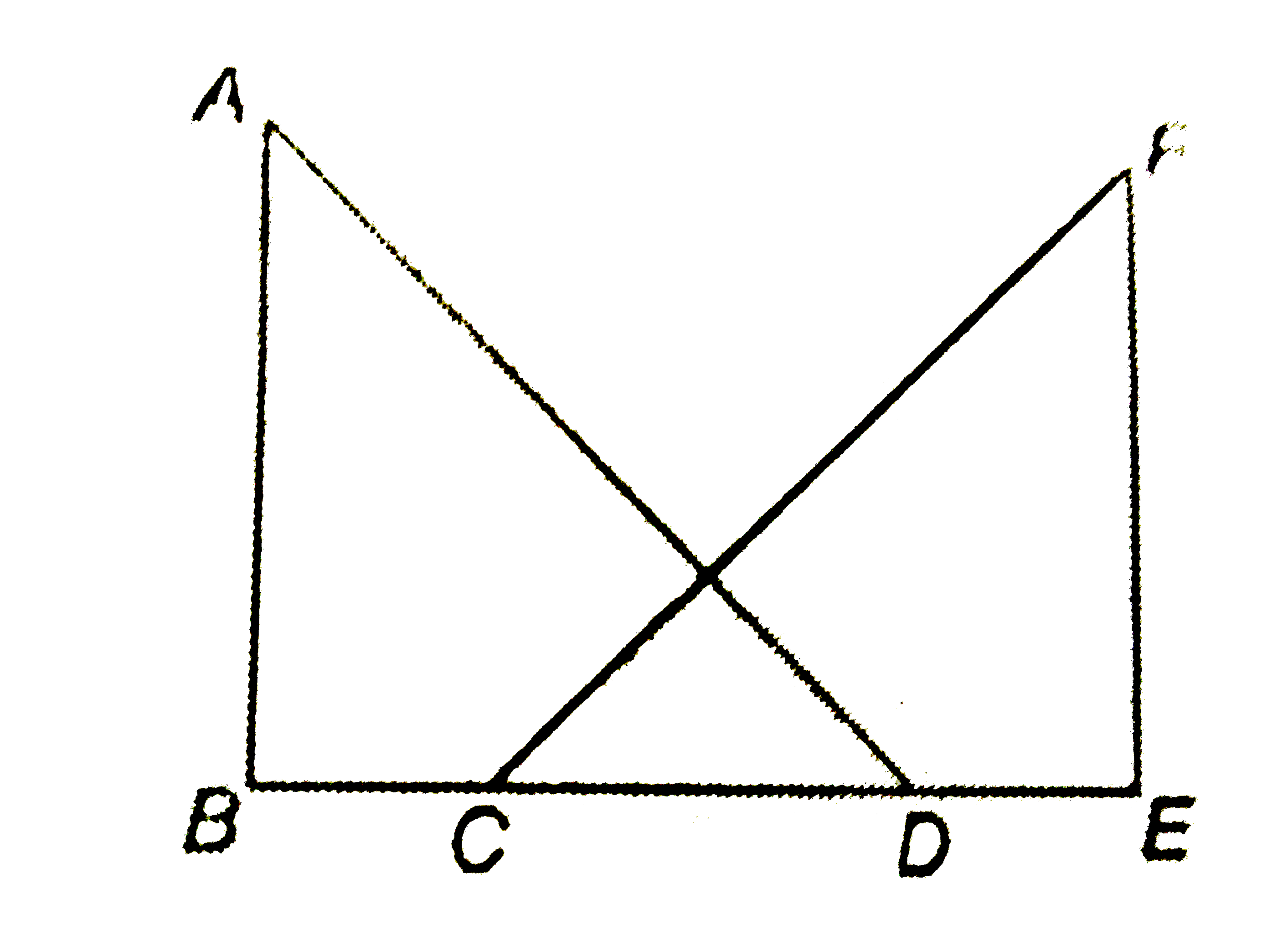
In the given figure, ∠ABC=80∘ and ∠DEF=45∘. The arms DE
and EF of ∠DEF cut BC at P and Q respectively, Prove that PD∣∣BA.

Let ∠EPQ=x∘
We known that the sum of the angles of a triangle is 180∘.
∴∠EPQ+∠PEQ+∠EQP=180∘
⇒∠EPQ+45∘+35∘=180∘
⇒∠EPQ=(180∘−80∘)=100∘.
Now, EPD is a straight line.
∴∠EPQ+∠DPQ=180∘⇒100∘+∠DPQ=180∘
⇒∠DPQ=(180∘−100∘)=80∘.
Thus, ∠ABP=∠DPQ [each equal to 80∘]
But, these are corresponding angles.
Hence, PD∣∣BA.
Topper's Solved these Questions
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7A
Explore 12 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7B
Explore 16 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Multiple Choice Questions (Mcq)
Explore 28 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Multiple Choice Questions (Mcq)
Explore 24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA Book:RS AGGARWALChapter:MEAN , MEDIAN AND MODE OF UNGROUPED DATA Exercise:Multiple Choice Questions (Mcq)
Explore 18 Videos
Similar Questions
In the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
View SolutionIn the figure, bisectors of ∠Band∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=1/2(∠ABC+∠ADC)
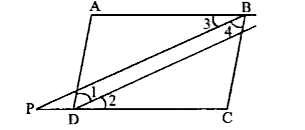
Given: In the given figure, bisectors of ∠Band∠D of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
To prove: ∠P+∠Q=12(∠ABC+∠ADC)
View Solution
Knowledge Check
In the given figure , DE∣∣BC,∠ABC=118∘,∠DAB=42∘ , then ∠ADE is equal to :
 A118∘B42∘C138∘D160∘
A118∘B42∘C138∘D160∘In the given figure AB||CDandEF||DQ. Find the value of ∠DEF:
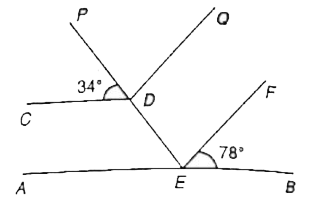 A68∘B78∘C34∘D39∘
A68∘B78∘C34∘D39∘
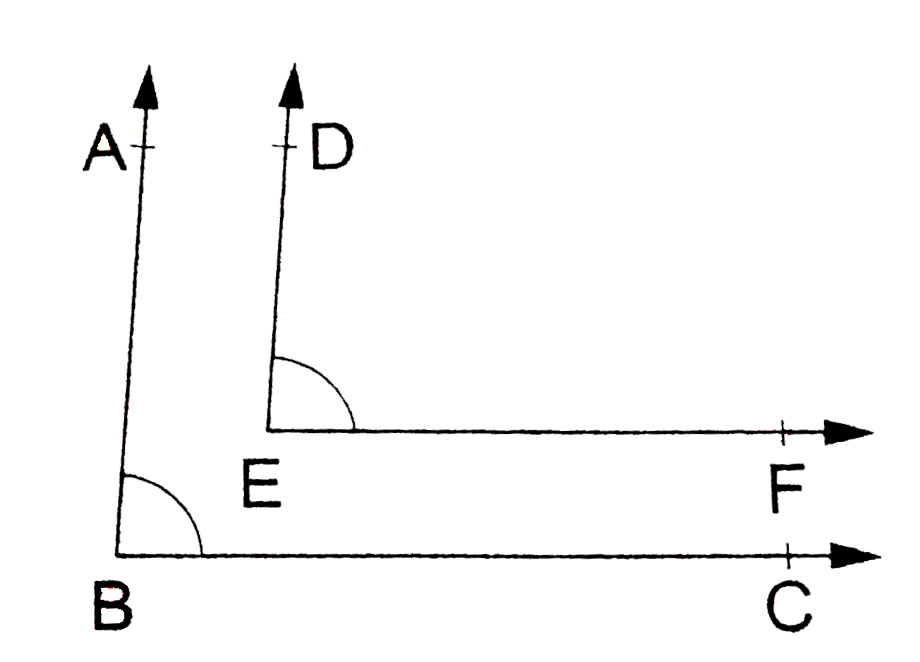
In the given figure, BA∣∣ED and BC∣∣EF. Show that ∠ABC=∠DEF.
View SolutionIn the adjoining figure, AB=EF,BC=DE,∠ABC=∠FED=90∘, prove that AD=CF.
View SolutionIn the given figure, AB∣∣DE. Prove that:
∠ABC+∠BCD=180∘+∠CDE.

View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.

View SolutionIn the given figure, ∠AMN=∠MBC=76∘ . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN in term of a,b and c.
View SolutionIn the given figure, BA∣∣ED and BC∣∣EF. Show that ∠ABC+∠DEF=180∘.
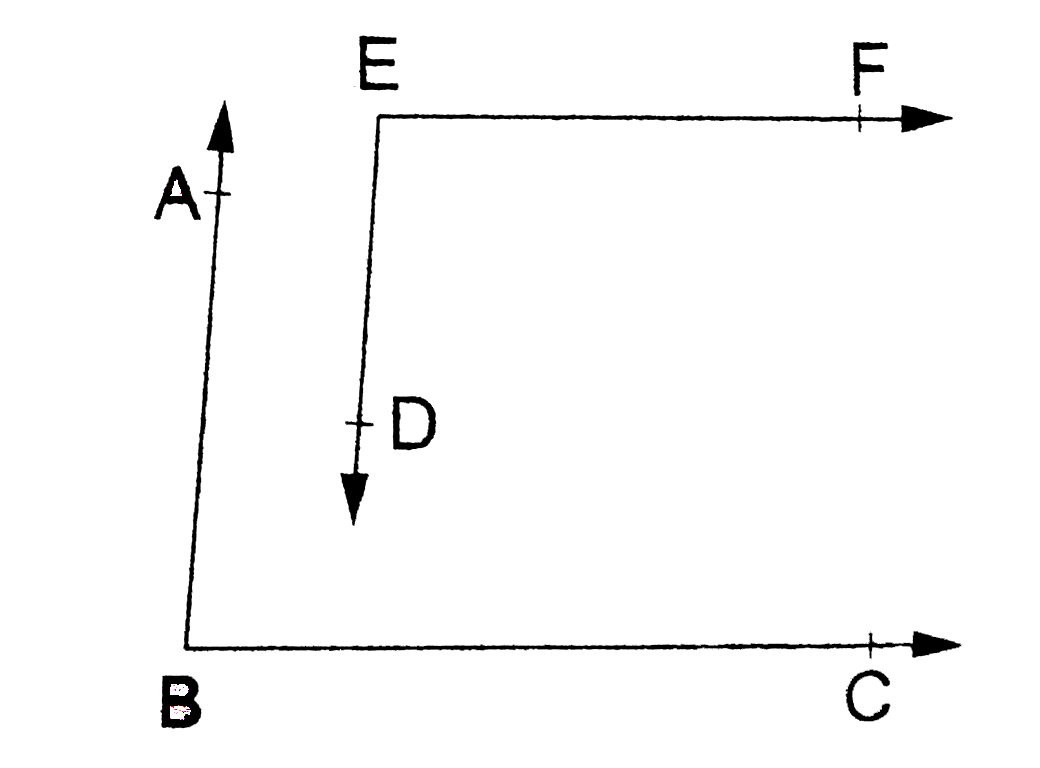
View Solution

