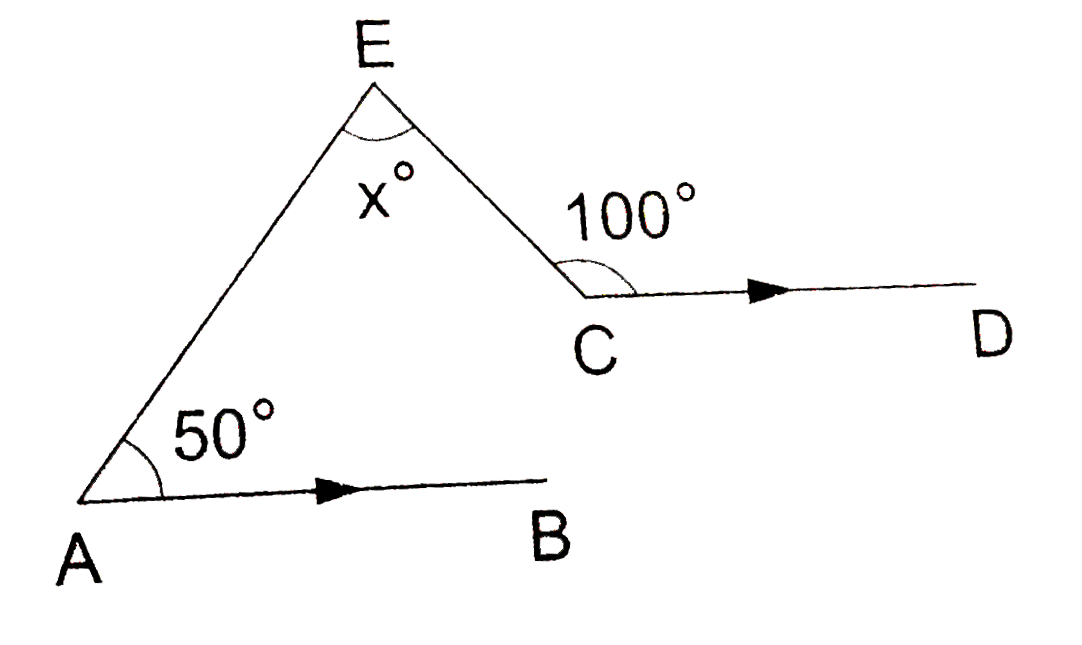
In the given figure, and . Find the value of x.
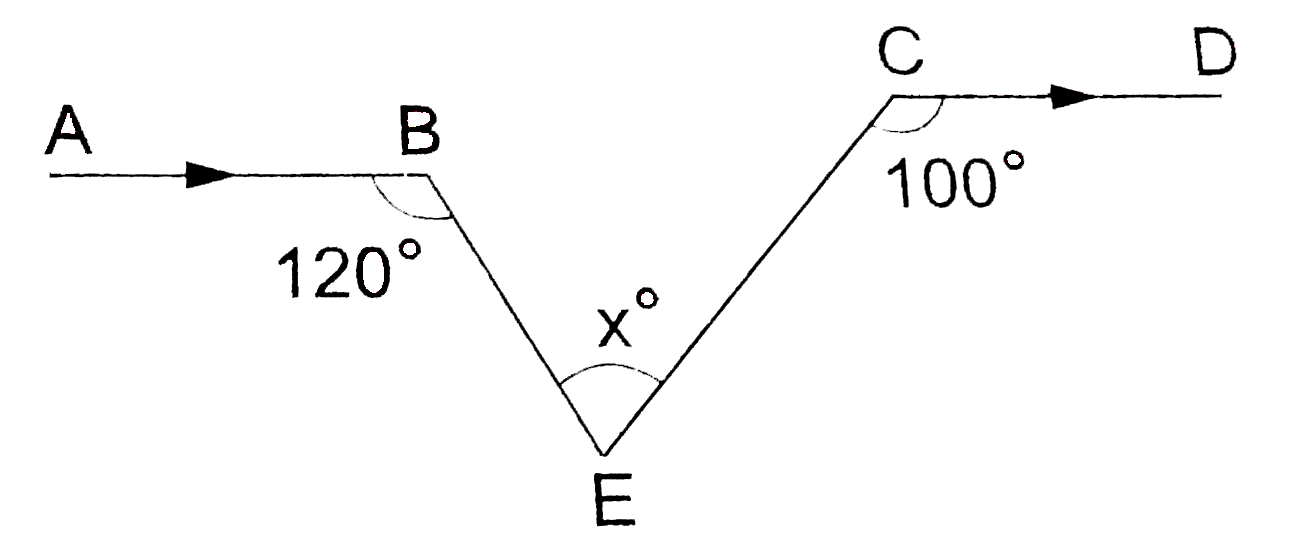
A
B
C
D
Video Solution
Text Solution
The correct Answer is:D
Through E, draw . Now, and BE is the transversal.
[co-interior ]
.
Again and CE is the transversal.
[co-interior ]
.
Now, FEG is a straight line.
.
Hence, .

|
Topper's Solved these Questions
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7A
Explore 12 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7B
Explore 16 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Multiple Choice Questions (Mcq)
Explore 28 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Multiple Choice Questions (Mcq)
Explore 24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA Book:RS AGGARWALChapter:MEAN , MEDIAN AND MODE OF UNGROUPED DATA Exercise:Multiple Choice Questions (Mcq)
Explore 18 Videos
Similar Questions
Knowledge Check
In the given figreu AB∣∣CD,∠BAD=30∘and∠ECD=50∘, find ∠CED
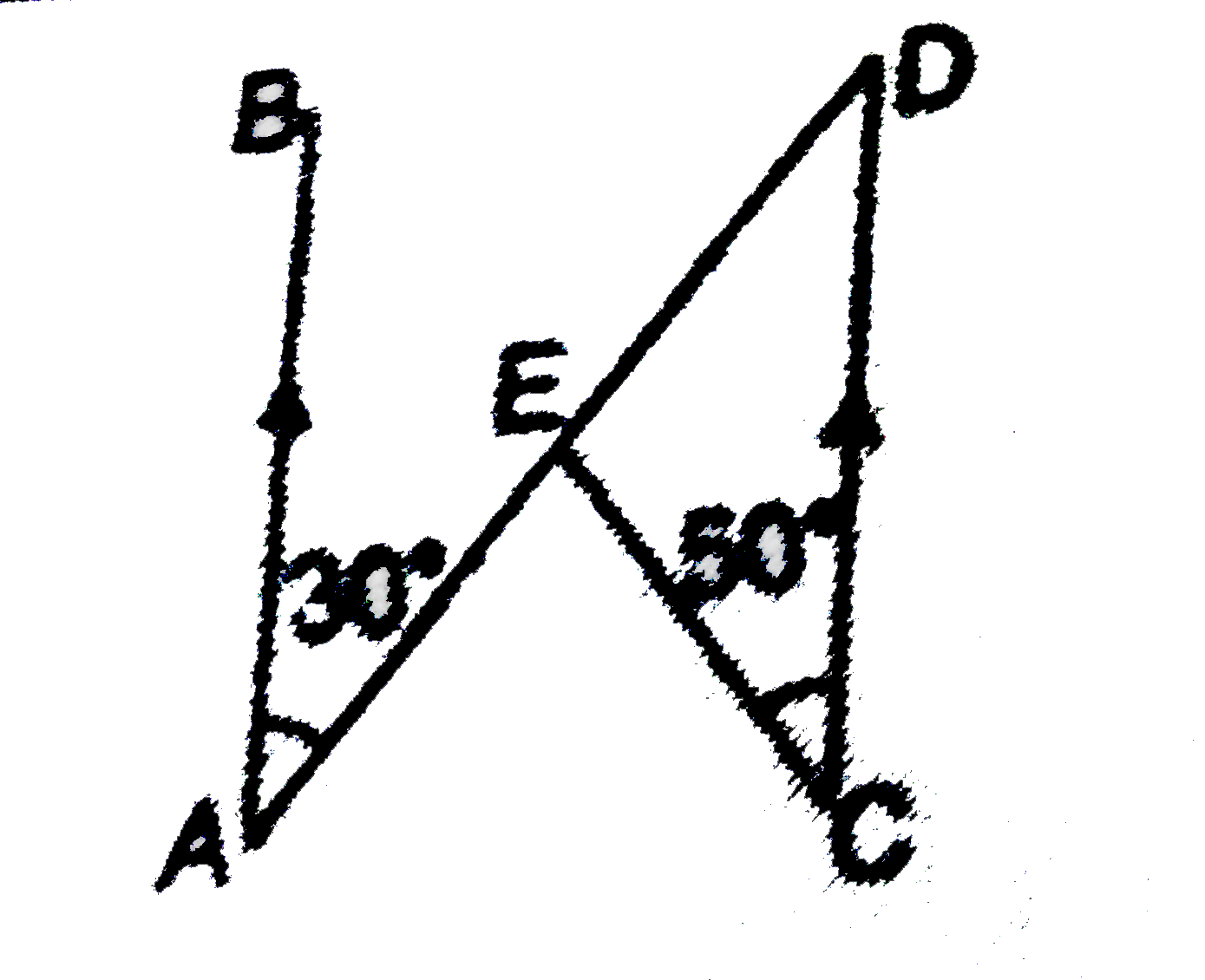 A120∘B30∘C100∘D50∘
A120∘B30∘C100∘D50∘In the given figure , AB∣∣CD. Find x.
 A26∘B13∘C23∘D46∘
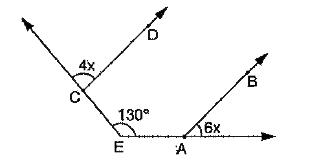
A26∘B13∘C23∘D46∘In the figure AB∣∣CD,∠ABE=100. Find ∠CDE:
 A125∘B55∘C65∘D75∘
A125∘B55∘C65∘D75∘
In the figure AB∣∣CD,∠ABE=100∘. Find ∠CDE:

View SolutionIn the given figure, AB∣∣CD. If ∠EAB=50∘ and ∠ECD=60∘ then ∠AEB=?

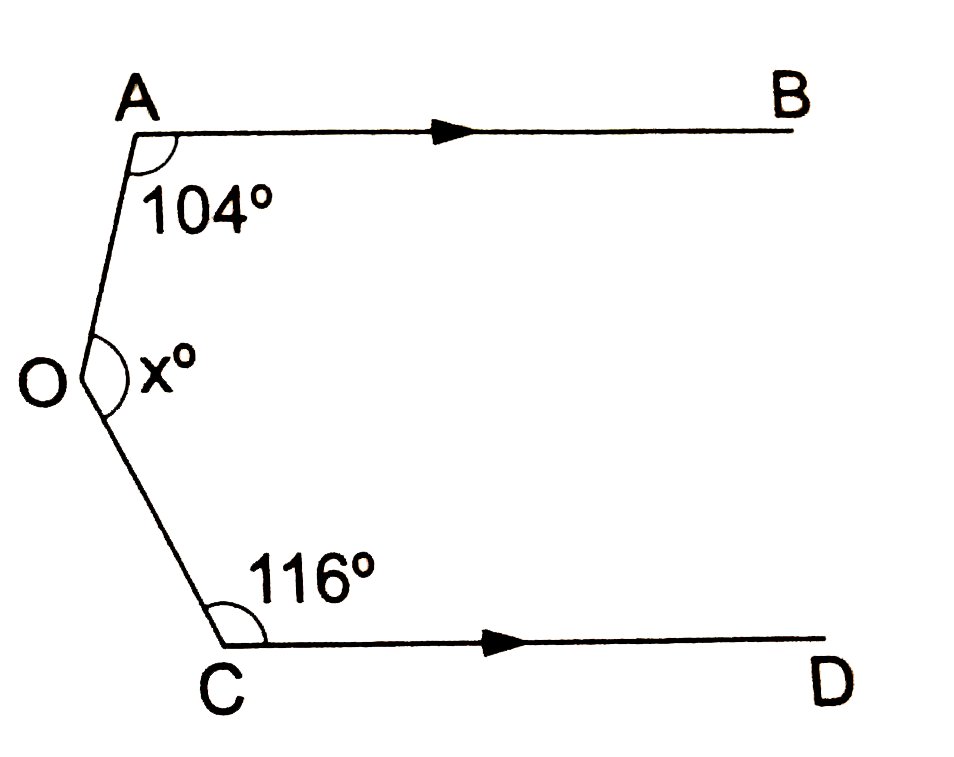
View SolutionIn the given figure, AB∣∣CD and ∠AOC=x∘. If ∠OAB=104∘ and ∠OCD=116∘, find the value of x.
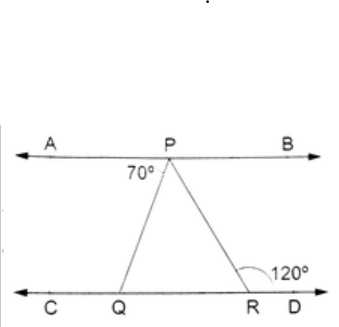
View SolutionIn the given figure, AB∣∣CD. If ∠APQ=70∘ and ∠PRD=120∘ then ∠QPR=?
<
View SolutionIn the given figure, AB∣∣CD. If ∠AOC=30∘ and ∠OAB=100∘ then ∠OCD=?

View Solution