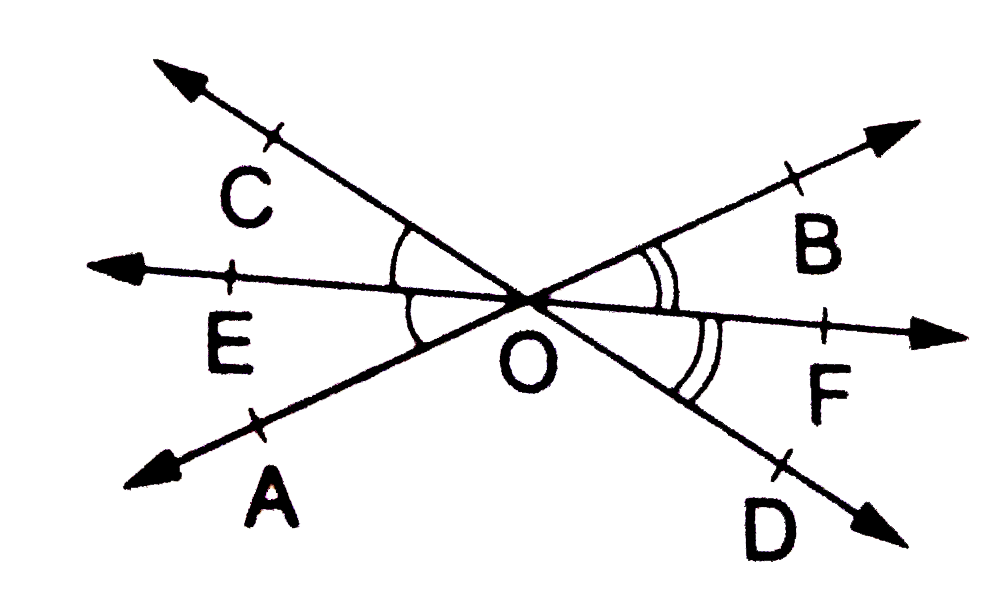
Prove that the bisectors of a pair of vertically opposite angles are in the same straight line.
GIVEN Two line AB and CD intersect at a point O. Also, OE and OF are th bisectors of ∠AOC and ∠BOD respectively.
TO PROVE EOF is a straight line.
PROOF Since the sum of all the angles around a point is 360∘, we have:
∠AOC+∠BOC+∠BOD+∠AOD=360∘
⇒∠AOC+2∠BOC+∠BOD=360∘
[∵∠AOD=∠BOC(vert. opp.∠s)]
⇒2∠EOC+2∠BOC+2∠BOF=360∘
[ ∵ OE is the bisector of ∠AOC and OF is the bisector of ∠BOD]
⇒∠EOC+∠BOC+∠BOF=180∘
⇒∠EOF=180∘, i.e. ∠EOF is a straight angle.
Hence, EOF is a straight line.
Topper's Solved these Questions
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Example
Explore 13 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 7A
Explore 12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:RS AGGARWALChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Multiple Choice Questions (Mcq)
Explore 24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA Book:RS AGGARWALChapter:MEAN , MEDIAN AND MODE OF UNGROUPED DATA Exercise:Multiple Choice Questions (Mcq)
Explore 18 Videos
Similar Questions
Vertically opposite angles are always
View SolutionProve that vertically opposite angles are equal.
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionA transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
View SolutionAngle between pair of straight line
View SolutionIf a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
View SolutionIf two lines intersect prove that the vertically opposite angles are equal
View SolutionProve that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionFill in the blanks:(i) If two angles are complementary, then the sum of their measures is _______.(ii) If two angles are supplementary, then the sum of their measures is ______.(iii) Two angles forming a linear pair are _______________.(iv) If two adjacent angles are supplementary, they form a ___________.(v) If two lines intersect at a point, then the vertically opposite angles are always_____________.(vi) If two lines intersect at a point, and if one pair of vertically opposite angles areacute angles, then the other pair of vertically opposite angles are __________.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View Solution

