In the given figure, O is the centre of a circle in which chords AB and CD intersect at P such that PO bisects ∠BPD. Prove that AB= CD .
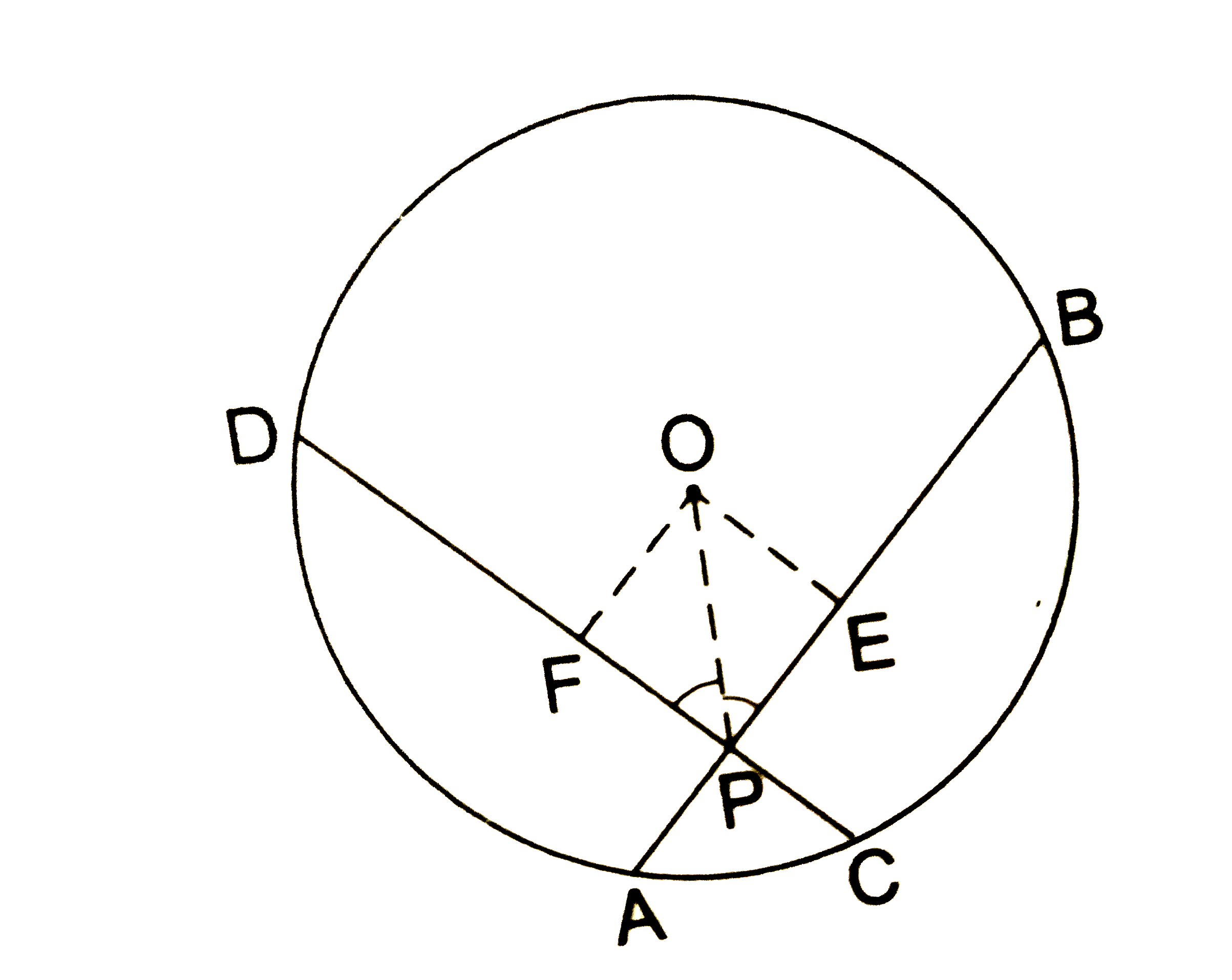
Draw OE⊥AB and OF⊥CD.
Then, ∠OEP=∠=90∘,OP=OP,∠OPE=∠OPF.
∴ΔOEP=≅ΔOFP, and hence OE=OE. And , chords which are equidistant from the centre are equal.
Similar Questions
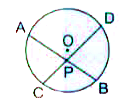
In the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 18 cm, PB = 8 cm, CP = 5 cm, then find the length of CD.
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
View SolutionIn the figure, P is the centre of the circle. Two chords AB and CD are parallel to each other. Prove ∠CPA=∠DPB.
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
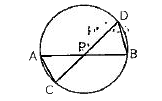
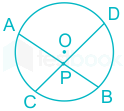
View SolutionIn Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
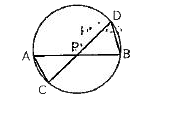
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
View SolutionIn the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View SolutionIn a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View Solution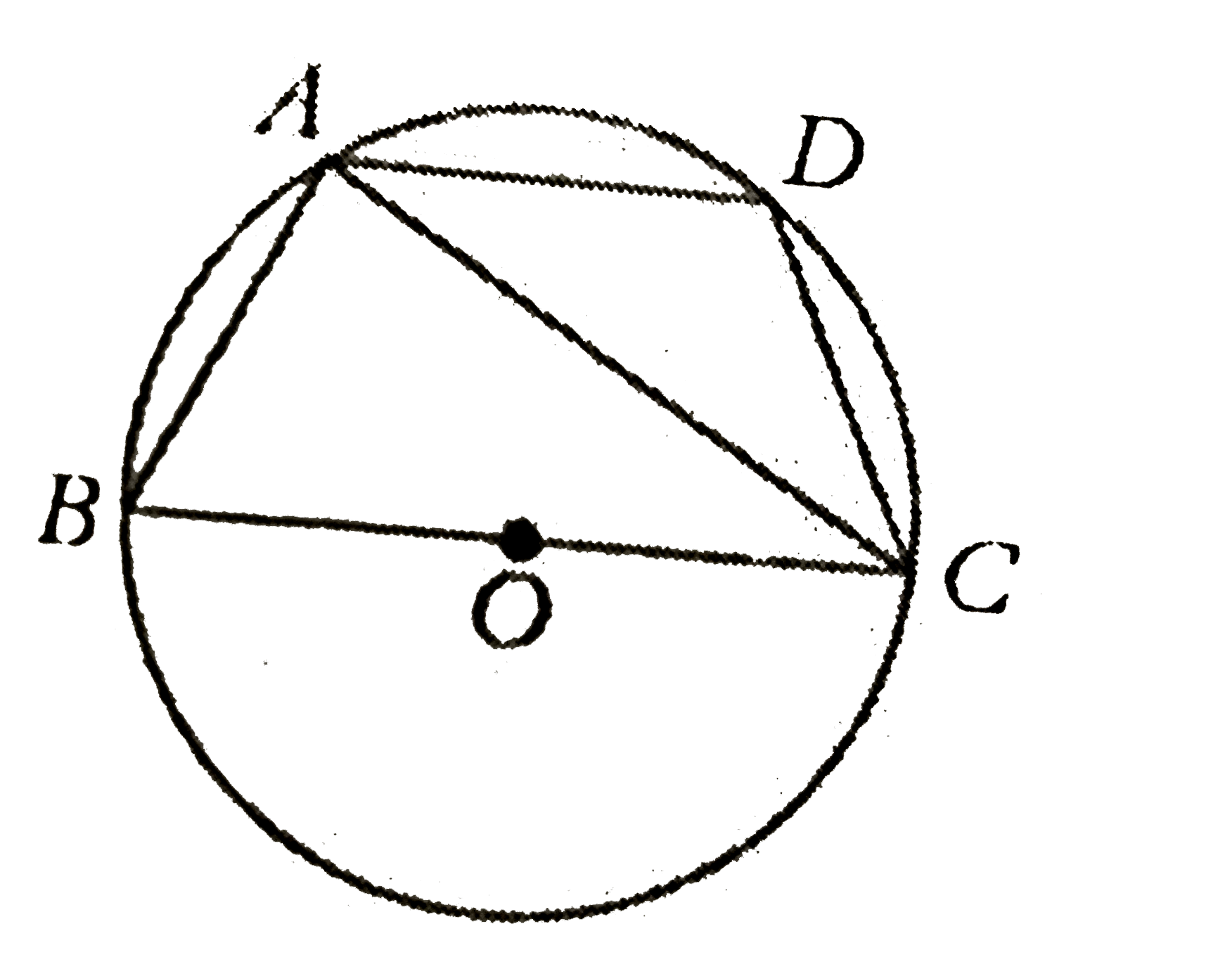
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
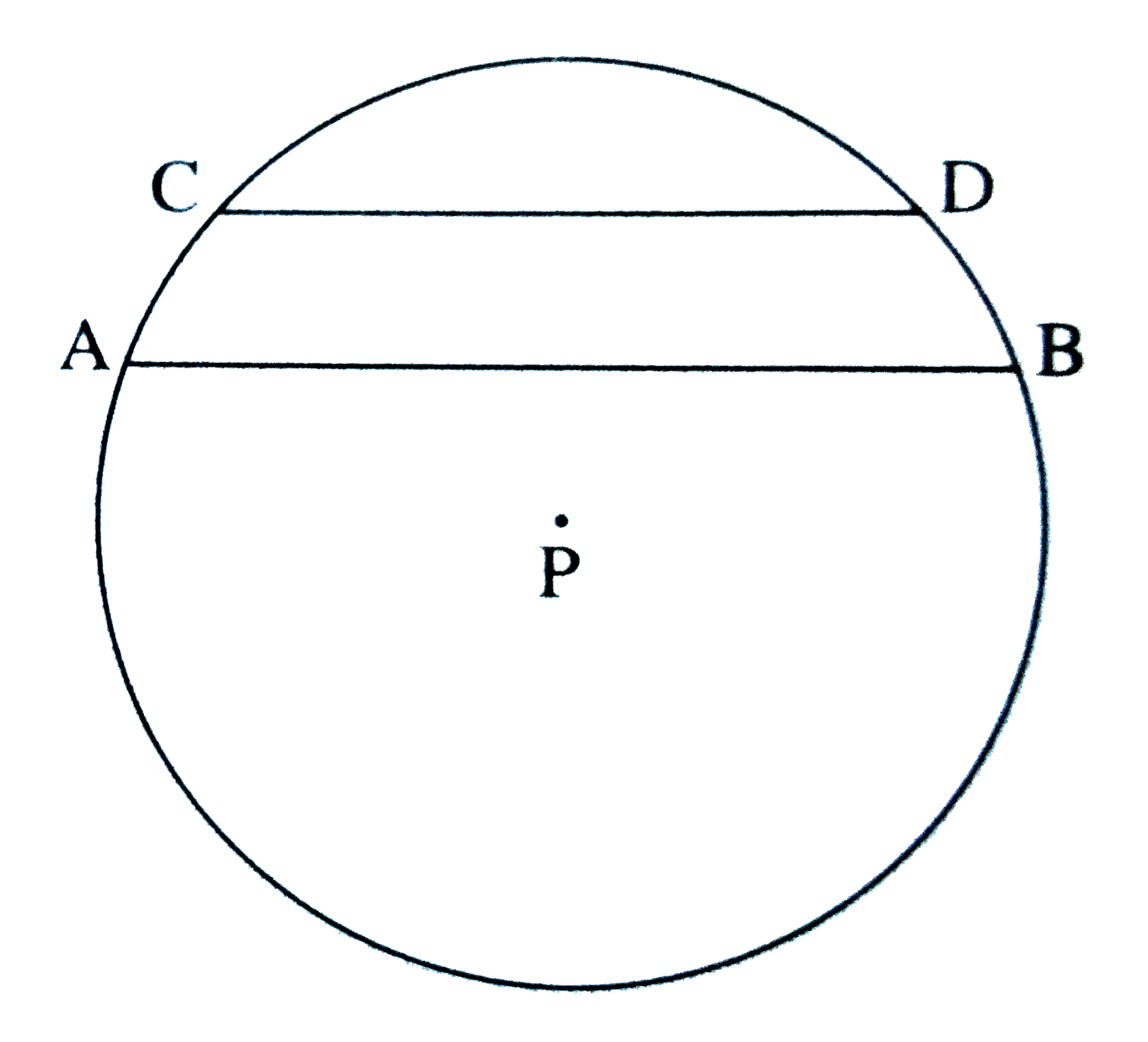
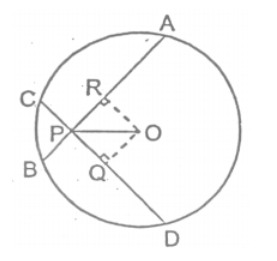
View SolutionIn the given figure, a straight line l passing through the centre O of the circle bisects the chord AB and CD. Prove that AB||CD.
View Solution
