Three metal rod A, B and C of same length and cross-section are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), then the effective thermal conductivity of the system will be
KX7
6KY7
7KY3
7KZ
The correct Answer is:B

Given KY=2KZ,KY=12KX
Let L and A be the length and area of cross-section of each rod respectively. Then
Thermal resistance of rod X, RX=LKXA
Thermal resistance of rod Y, RY=LKYA
Thermal resistance of rod Z, RZ=LKZA
The electrical equivalent circuit is as shown in the figure.

Here, the rods are connected in series
∴RS=RX+RY+RZ
or 3lKeqA=LKXA+LKYA+LKZA
or 3Keq=12KY+1KY+2KY=1+2+42KY=72KY
or Keq=67KY
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:Check Your Neet Vitals
Explore 22 Videos
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:AIPMT/NEET (MCQs)
Explore 40 Videos
- PROPERTIES OF BULK MATTERBook:MTG GUIDEChapter:PROPERTIES OF BULK MATTERExercise:AIPMT/NEET (MCQs)
Explore 40 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:MTG GUIDEChapter:PHYSICAL WORLD AND MEASUREMENTExercise:AIPMT / NEET MCQ
Explore 14 Videos
- THERMODYNAMICSBook:MTG GUIDEChapter:THERMODYNAMICSExercise:AIPMT/NEET (MCQs)
Explore 26 Videos
Similar Questions
Three identical metal rods A, B and C are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), (KA=49w/mK) calculate the effective thermal conductivity of the system ?
View Solution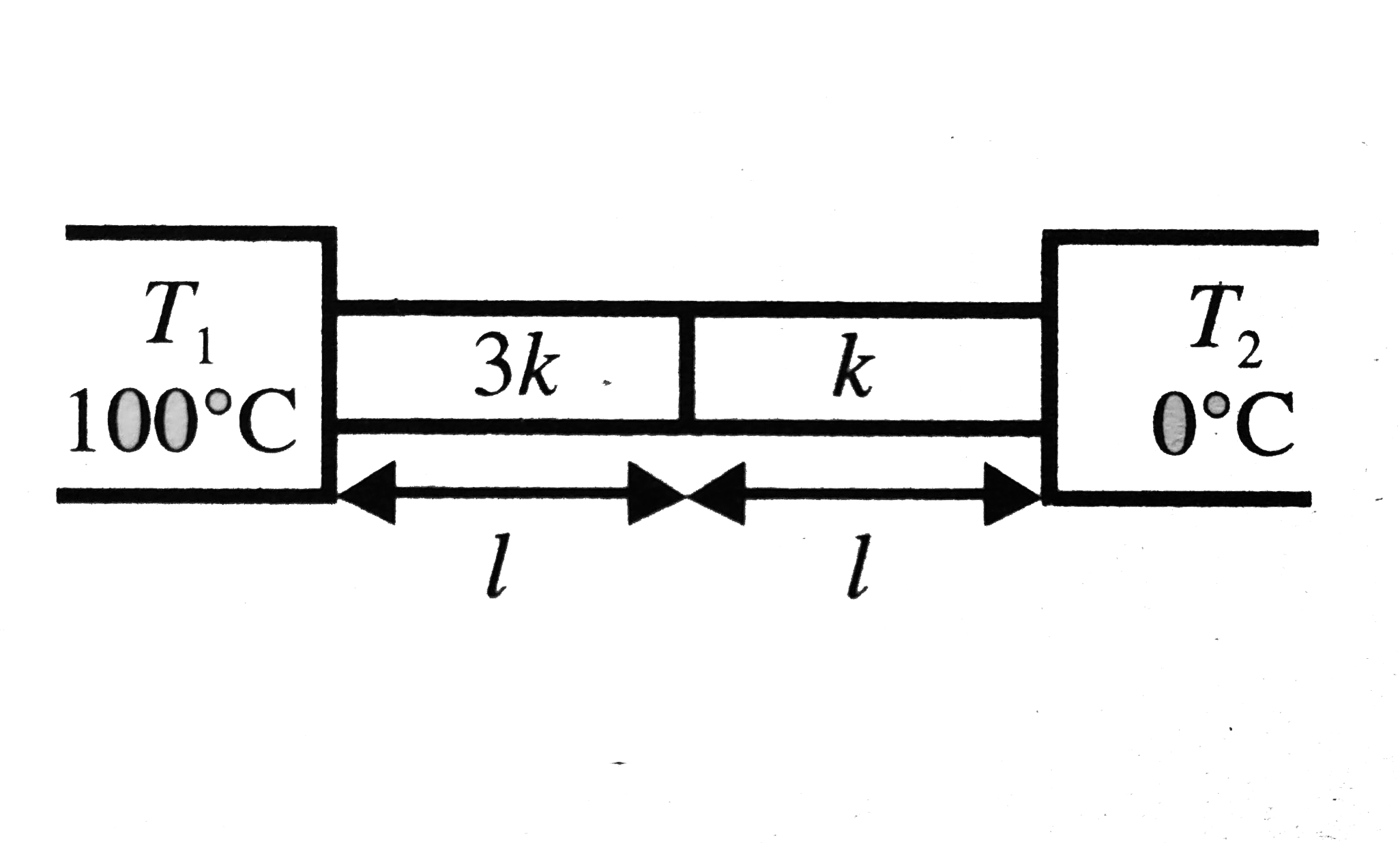
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View Solution
Knowledge Check
Three identical rods A, B and C are placed end to end. A temperature difference is maintained between the free ends of A and C. The thermal conductitvity of B is thrice that of C and half that of A. The effective thermal conductivity of rod A)
A13KAB3KAC2KAD23KATwo conducting rods A and B of same length and cross-sectional area are connected (i) In series (ii) In parallel as shown. In both combination a temperature difference of 100°C is maintained. If thermal conductivity of A is 3 K and that of B is K then the ratio of heat current flowing in parallel combination to that flowing in series combination is
 A163B316C11D13
A163B316C11D13Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)K
In the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a)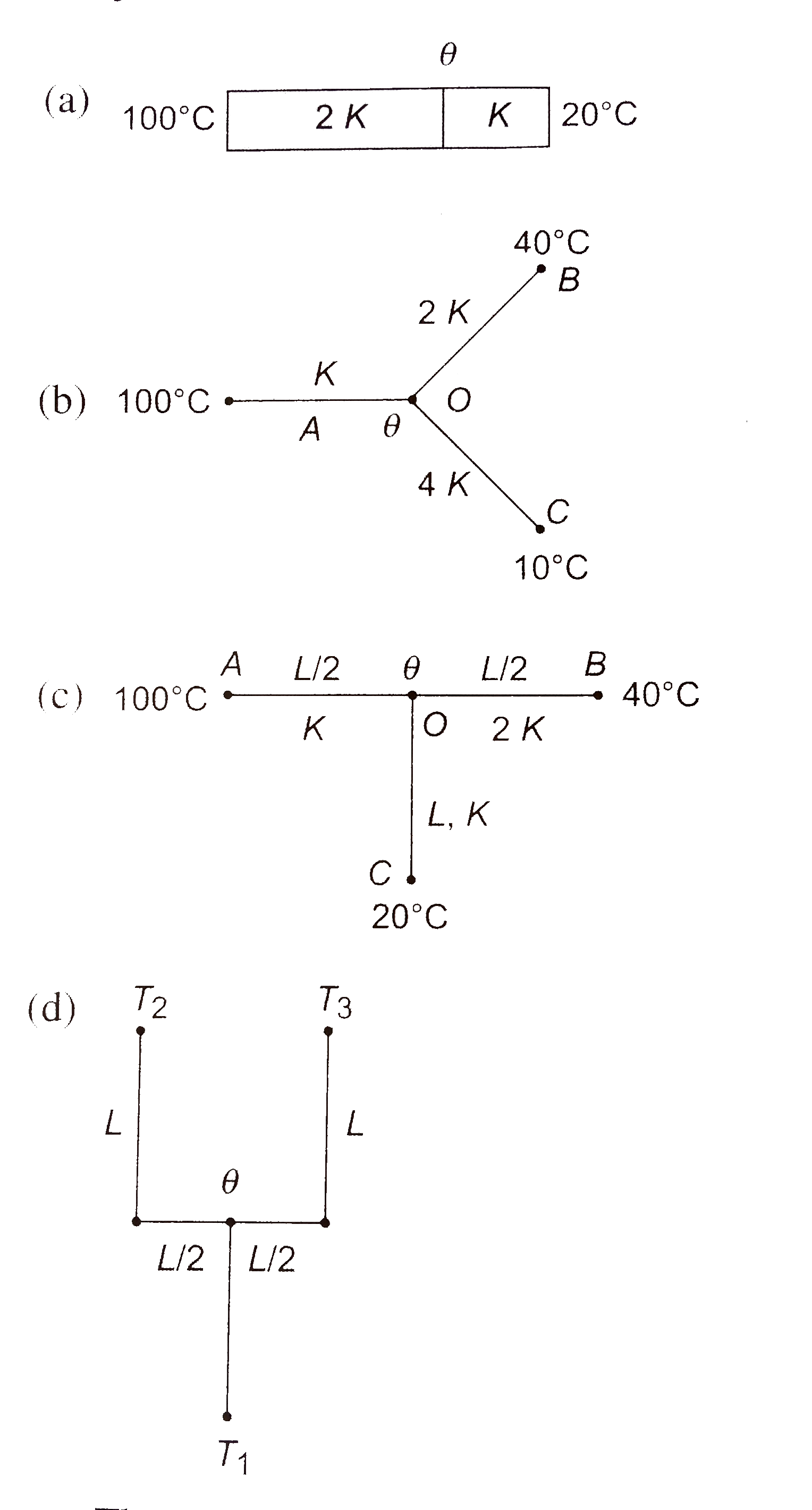
(b)
(c )
(d)
The thermal conductivity of each rod is K.
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionTwo rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View Solution