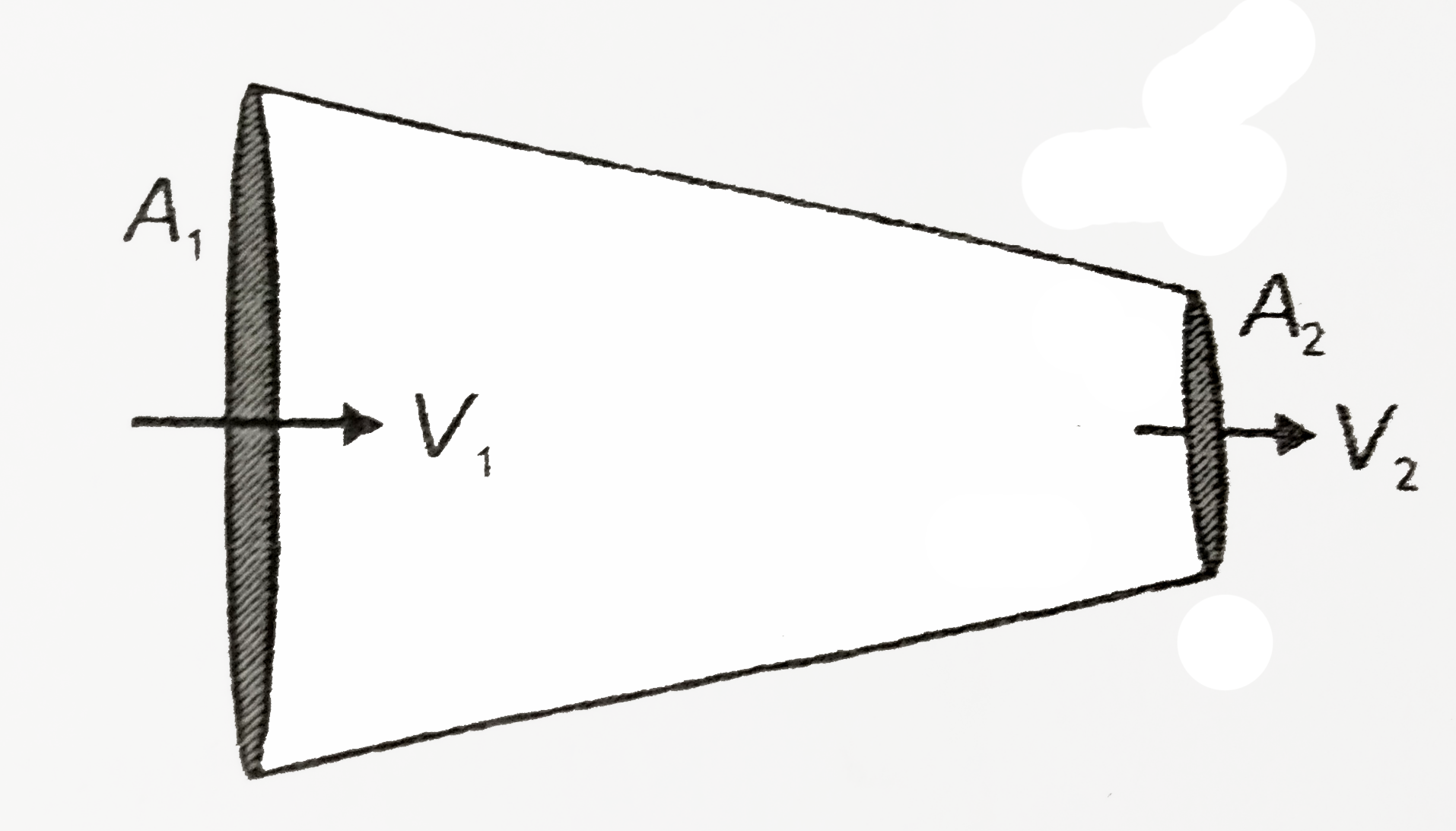
Calculate the rate of flow of glycerine of density 1.25×103kg/m3 through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is 10N/m2.
5.28×10−4m3/s
6.28×10−4m3/s
7.28×10−4m3/s
8.28×10−4m3/s
The correct Answer is:B
According to equation of continuity
v2v1=A1A2=π×(0.1)2π(0.04)2=254 …(i)
According to Bernoulli.s equation for horizontal tube,
P1+12ρv21=P2+12ρv22
or v22−v21=2(P1−P2)ρ
or v22−v21=(2×10)(1.25×103)=16×10−3...(ii)
Substituting the value of v2 from equation (i) in (ii), we get
(6.25v1)2−v21=16×10−3orv1=0.02m/s
So rate of flow through the tube =A1v1=(A2v2)=π×(0.1)2×0.02=6.28×10−4m3/s

Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals
22 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
Calculate the rate of flow of glycerine of density. 1.25×103kg/m3 through the conical section of a pipe. If the radii of its ends are 1.0m and 0.04m and the pressure drop across its length is 10N/m2.
View SolutionCalculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View Solution
Knowledge Check
The radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
A0.04 mB0.4 mC4mD40 mThe workdone by pressure in forcing 1m3 of water through a pipe if the pressure difference across the pipe is 104 Pa, is
A105JB104JC103JD102JTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
A25 cmB15 cmC5 cmD20 cm
Calculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
View SolutionCalculate the moment of inertia of a cylinder of length 1.5m, radius 0.05m and density 8×103kg/m3 about the axis of the cylinder.
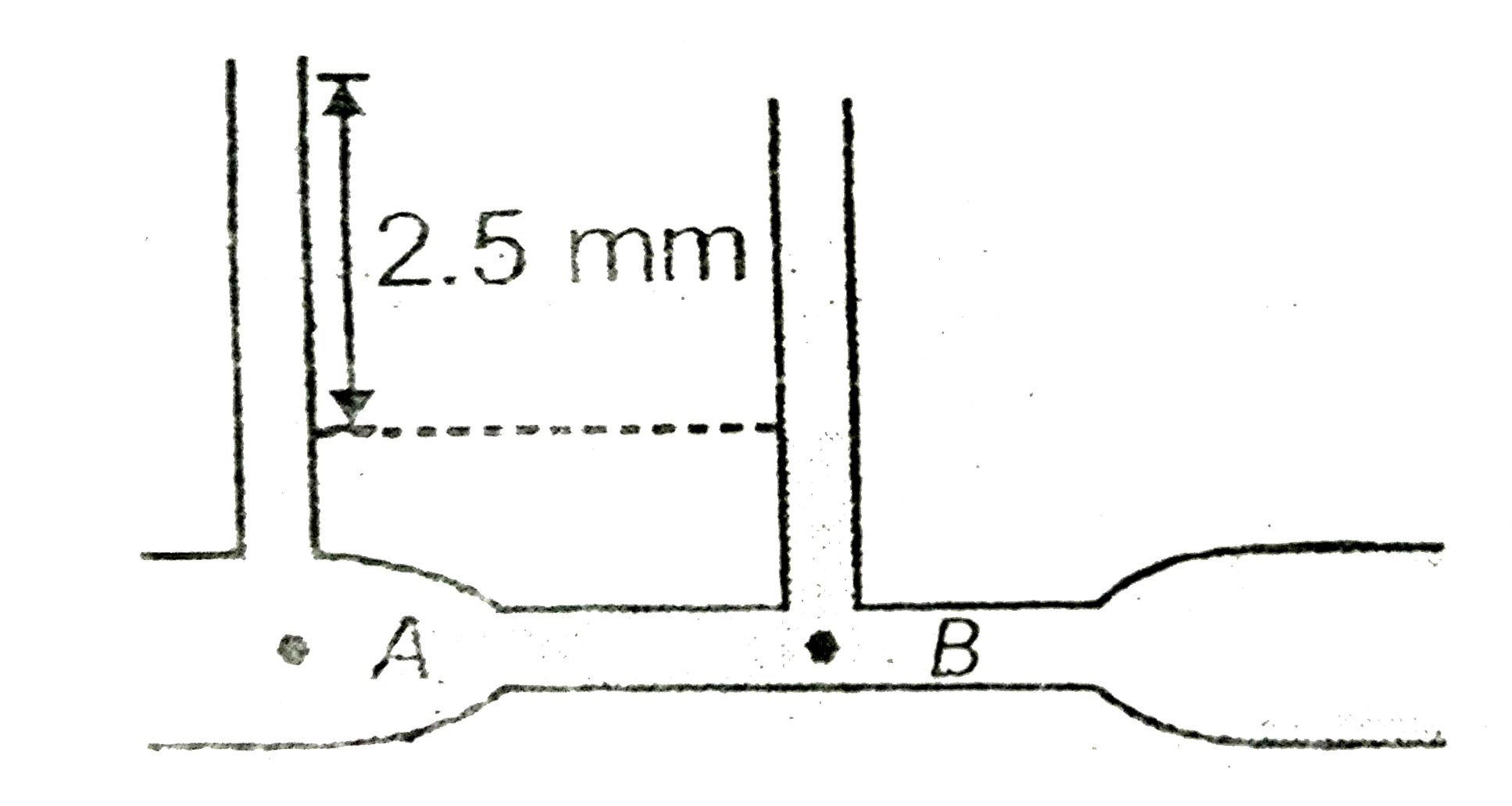
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionCalculate the rate of flow (volume per second) of a liquid through a capillary tube of diameter 0.20×10−3m and length 1m,η=3.00×10−5Nm−2s and pressure gradient = 10 atm.
View SolutionCalculate the speed of a transverse wave in a wire of 1.0mm2 cross-section under a tension of 0.98N. Density of the material of wire is 9.8×103kg/m3
View Solution
