The rate of flow of liquid through a capillary tube of radius r is V, when the pressure difference across the two ends of the capillary is p. If pressure is increased by 3p and radius is reduced to r/2, then the rate of flow becomes
V8
V4
V2
V9
The correct Answer is:B
According to Poiseuille.s equation
V=πPr48ηl …(i)
V.=π(4P)(r2)48ηl …(ii)
Divide (ii) by (i), we get V.V=416=14orV.=V4
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals
22 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PROPERTIES OF BULK MATTERBOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)
40 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
Water flows in a stream line manner through a capillary tube of radius a. The pressure difference being P and the rate of flow is Q. If the radius is reduced to a4 and the pressure is increased to 4P. then the rate of flow becomes
View SolutionWhen water flows at a rate Q through a capillary tube of radius r placed horizontally a pressure difference p develops across the ends of the tube. If the radius of the tube is doubled and the rate of flow halved the pressure difference becomes
View Solution
Knowledge Check
The rate of flow of a liquid through a capillary tube is
Adirectly proportional to the length of tube.Binversely proportional to the difference of pressure between the ends of the tube.Cdirectly proportional to the 4th power of the radius of the tube.Dindependent of the nature of the liquid.Water flows in a stream line manner through a capillary tube of radius a. the pressure difference being P and the rate of the flows is Q. If the radius is reduced to a4 and the pressure is increased to 4P, then the rate of flow becomes
AQ2=64QBQ2=Q/64CQ2=Q/32DQ2=Q/16The rate of flow of liquid through a capillary tube in an experiment to determine the viscosity of the liquid increases
Awhen the pressure of the tube is increasedBwhen the length of the tube is increasedCwhen the radius of the tube is decreasedDnone of the above
Water flows in a streamline manner through a cappilary tube of radius a. The pressure difference being P and the rate of flow is Q . If the radius is reduced to a/2 and the pressure difference is increased to 2P, then find the rate of flow.
View SolutionThe rate of flow of liquid through a capillary tube of length l and radius r is Q at a constant pressure p. The rate of flow of liquid through a capillary tube of radius r2 and length 21 at the same pressure head will be_____
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
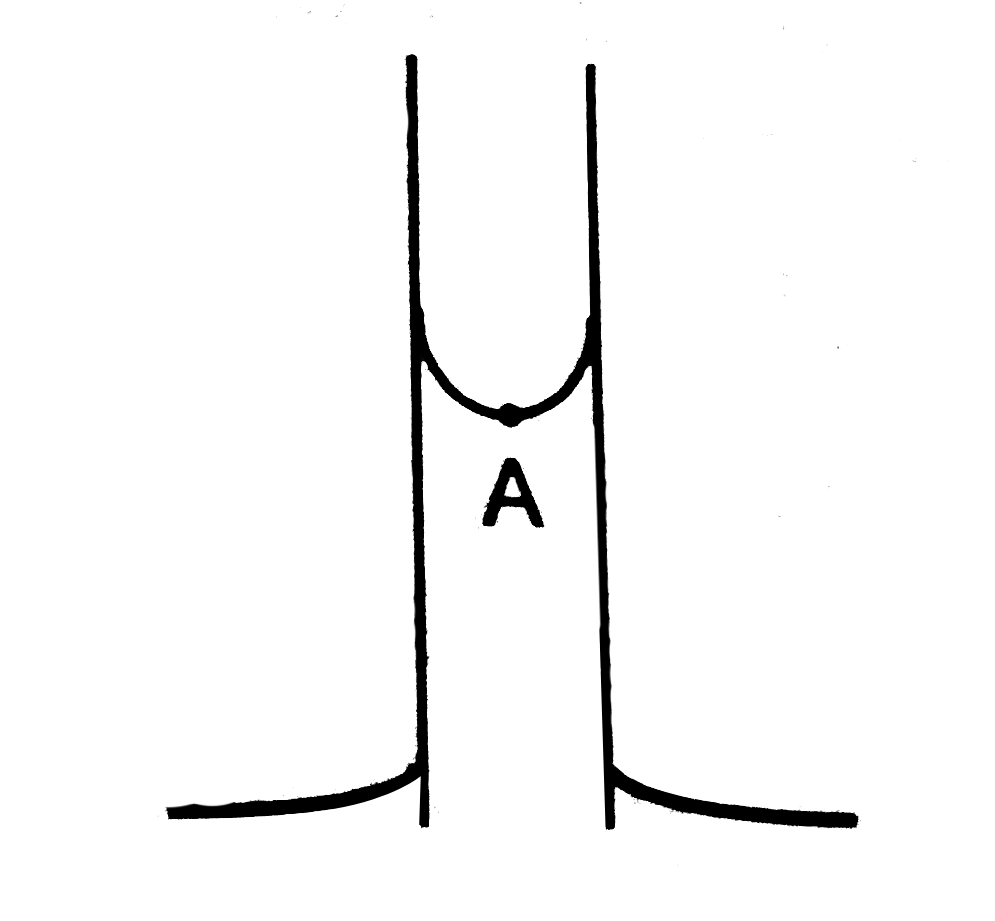
View SolutionIf Q is the rate of flow of liquid through a capillary tube of length l and radius r at constant pressure P, then the rate of flow of liquid through a capillary head is
View SolutionThe rate of flow of liquid ina tube of radius r, length l, whose ends are maintained at a pressure difference P is V=πQPr4ηl where η is coefficient of the viscosity and Q is
View Solution
