Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface. Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Let us consider a point P on the axis of the disc at a distance x from the centre of the disc. Let the disc is divided into a numerous charged rings as shown in figure.

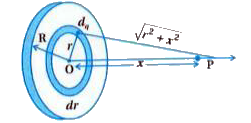
Let radius of ring r width dr and charges dq
$∴ Σ d A = σ 2 π r d r$
Potential at P
$d V = \frac{k d q}{r}$
charge on the ring dq = $+ σ [π {(r + d r)}^{2} - π r^{2}]$
$∴ d q = + σ π [{(r + d r)}^{2} - r^{2}]$
$= + σ π [r^{2} + 2 r d r + d r^{2} - r^{2}]$
$= + σ π [2 r d r + d r^{2}]$
Neglecting $d r^{2}$ as dr is very small
dq = $2 π r σ d r$
and dV = $\frac{k d q}{\sqrt{r^{2} + x^{2}}}$
$= \frac{k \times 2 π r σ d r}{\sqrt{r^{2} + x^{2}}}$ [From equation (2)]
$∴ V = 2 π k σ \int_{0}^{R} \frac{r d r}{\sqrt{r^{2} + x^{2}}} = 2 π k σ \int_{0}^{R} (r^{2} + x^{2}) (- 1 / 2) r d r$
$∴ V = 2 π k σ {[{(r^{2} + x^{2})}^{1 / 2} - x]}_{0}^{1 / 2}$
$∴ V = \frac{2 π σ}{4 π \in_{0}} [{(R^{2} + x^{2})}^{1 / 2} - x]$
$∴ V = \frac{2 π \times Q}{4 π \in_{0} \times π R^{2}} [\sqrt{{(R^{2} + x^{2})}^{1 / 2}} - x]$
$∴ V = \frac{2 Q}{4 π \in n_{0} R^{2}} [\sqrt{{(R^{2} + x^{2})}^{1 / 2}} - x]$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Section C ( NCERT Exemplar Solution ) ( Long Answer Type Questions )

Home
Ask Doubt
Profile