An electric dipole coincides on Z-axis and its mid point is on origin of the co-ordinate system. The electric field at an axial point at a distance z from origin is →Ez and electric field at an equatorial point at a distance y from origin is →Ey
Here, z=y>>a, so ∣∣→Ex∣∣∣∣→Ey∣∣=...............Solution in Gujrati
3
2
1
4
The correct Answer is:B
On the axis of dipole =∫2π0λadθ
=∫2π0cos2θdθ=aλ0π=πaλ0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS ASKED IN CBSE-PMT AIPMT NEET)
Explore 8 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:KUMAR PRAKASHANChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section-D (MCQs asked in GUJCET/Board Exam)
Explore 1 Video
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D MCQs (MCQs asked in Competitive Exams )
Explore 38 Videos
Similar Questions
A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionMass of photon in motion is ………
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionA and B are two points on the axis and the perpendicular bisector, reapectively, of and electric dipole. A and B are far away from the dipole and at equal distance from it. The fields at A and B are vecE_(A) and vecE_(B) . Then
View SolutionA point charge μ is placed at origin. Let →EA,→EB,and→EC be the electirc field at three points A (1,2,3), B (1,1,-1), and C(2,2,2) due to charge μ. Then
View SolutionAn electric dipole coincides on Z-axis and its mid-point is on origin of the coordinates system. The electric field at an axial point at a distance z from origin is E_((z)) and electric field at an equatorial point at a distance y from origin is E_((y)) . Here, z = y gt gt a , so |(E_((z)))/(E_((y)))| = ...
View SolutionConsider a sphere of radius R which carries a uniform charge density rho . If a sphere of radius R/2 is carved out of it,as shown, the ratio (vecE_(A))/(vecE_(B)) of magnetic of electric field vecE_(a) and vecE_(B) , respectively, at points A and B due to the remaining portion is:
View Solutionएक वैधुत द्विध्रुव की अक्ष पर, वैधुत द्विध्रुव से दुरी r पर वैधुत क्षेत्र की तीव्रता →E1 है तथा निरक्षीय रेखा पर वैधुत द्विध्रुव से दुरी 2r पर वैधुत क्षेत्र की तीव्रता →E2 है। तब-
View SolutionP and Q are two points on the axis and the perpendicular bisector respectively of an electric dipole. Both the points are far way from the dipole, and at equal distances from it. If →EP and →EQ are fields at P and Q ten
View Solutionएक वैद्युत द्विध्रुव z - अक्ष से सम्पाती है तथा इसका मध्य बिन्दु मूल बिन्दु पर स्थित है | इसके अक्षीय स्थिति में मूल बिन्दु से z दूरी पर वैद्युत क्षेत्र की तीव्रता →E(z) और निरक्षीय स्थिति में मूलबिन्दु से y दूरी वैद्युत क्षेत्र की तीव्रता →E(y) जहाँ पर z=y>>a, तब ∣∣ ∣∣→E(z)→E(y)∣∣ ∣∣=..... का मान होगा
View Solutionx−y तल में किसी बिन्दु (x,y) पर विद्युतीय विभव V=−kxy द्वारा दिया गया है | मूल बिन्दु से दूरी पर विद्युत क्षेत्र की तीव्रता निम्न रूप में परिवर्तित होती है
View SolutionElectrostatic potential at one point is V. Then electric field along X-axis can be written as vecE_(x) =...........
View SolutionConsider a sphere of radius R which carries a uniform charge density ρ. If a sphere of radius R2 is carved out of it,as shown, the ratio →EA→EB of magnitude of electric field →Ea and →EB, respectively, at points A and B due to the remaining portion is:
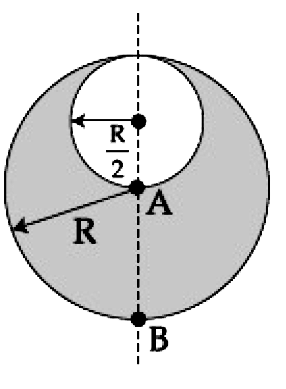
View SolutionIf →Eax and →Eeq represent electric field at a point on the axial and equatorial line of dipole. If points are at a distance r from the centre of the dipole, for r⟩a
View SolutionAn electric dipole coincides on Z-axis and its mid-point is on origin of the coordinates system. The electric field at an axial point at a distance z from origin is E(z) and electric field at an equatorial point at a distance y from origin is E(y). Here, z=y>>a, so ∣∣∣E(z)E(y)∣∣∣=... 1 4 3 2
View Solution