एक वैद्युत द्विध्रुव z - अक्ष से सम्पाती है तथा इसका मध्य बिन्दु मूल बिन्दु पर स्थित है | इसके अक्षीय स्थिति में मूल बिन्दु से z दूरी पर वैद्युत क्षेत्र की तीव्रता →E(z) और निरक्षीय स्थिति में मूलबिन्दु से y दूरी वैद्युत क्षेत्र की तीव्रता →E(y) जहाँ पर z=y>>a, तब ∣∣ ∣∣→E(z)→E(y)∣∣ ∣∣=..... का मान होगा
1
4
3
2
The correct Answer is:D
मूल बिंदु से अक्षीय स्थिति में z दुरी पर बिंदु P पर वैद्युत क्षेत्र की तीव्रता का परिमाण
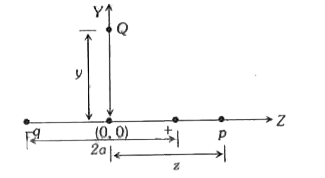
∣∣→E(z)∣∣4qaz4πε0(z2−a2)2=2pz4πε0(z2−a2)2
जहाँ पर p=2qa वैद्युत द्विध्रुव आघूर्ण है
जहाँ z>>a.∣∣→E(z)∣∣=2p4πε0z3
मूल बिंदु से निरक्षीय स्थिति में y दुरी पर बिंदु पर Q पर वैद्युत क्षेत्र की तीव्रता
∣∣
∣∣→E)((y))∣=14πε02qa(y2+a2)3/2=p4πε0(y2+a2)3/2
जब y>>a,∣∣→E(y)∣∣=p4πε0y3
ओर जब z=y>>a
∴ ∣∣→E(z)∣∣∣∣E(y)∣∣=2
Topper's Solved these Questions
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (विद्युत फ्लक्स एवं गॉस नियम)
37 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (धारिता)
128 Videos
- स्थिर वैद्युतBOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (विद्युत क्षेत्र एवं विभव )
207 Videos
- सरल आवर्त गति BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )
19 Videos
Similar Questions
R त्रिज्या तथा L लम्बाई के एक बेलन को एकसमान वैद्युत क्षेत्र E के अनुदिश अक्ष में रखा गया है , तो बेलन के पृष्ठ से सम्पूर्ण फ्लक्स हेतु व्यंजक
View Solutionएक आवेशित समांतर प्लेट संधारित्र की स्थितिज ऊर्जा U0 है | यदि प्लेटों के मध्य एक k परावैद्युतांक पदार्थ की पट्टिका रख दी जाती है तो संधारित्र की नई स्थितिज ऊर्जा होगी
View Solutionदो समान आवेश Q परस्पर कुछ दूरी पर रखे हैं इनको मिलाने वाली रेखा के केन्द्र पर q आवेश रखा गया है | तीनों आवेशों का निकाय सन्तुलन में होगा यदि का q मान हो
View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ ||
View Solutionवैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionवैद्युत क्षेत्र में वैद्युत द्विध्रुव | बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ
View Solutionआवेशों के निकाय के कारण विद्युत क्षेत्र || वैद्युत द्विध्रुव तथा द्विध्रुव का आघूर्ण || वैद्युत द्विध्रुव के कारण क्षेत्र अक्षीय स्थिति में || कुछ प्रश्न
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionवैद्युत द्विध्रुव के कारण अक्षीय स्थिति में विद्युत् क्षेत्र
View Solutionवैद्युत द्विध्रुव के कारण निरक्षीय स्थिति में विद्युत् क्षेत्र
View Solutionरिक्त स्थानों की पूर्ति कीजिए -
मूल बिन्दु 0 से समतल →r.→N=d की दूरी ............... है।
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionवैद्युत द्विध्रव प्रश्न|वैद्युत द्विध्रव के कारण निरक्षीय स्थिति में वैद्युत क्षेत्र|OMR|Summary
View Solution
