A uniform sphere is projected horizontally with a purely translatory motion with initial velocity of 7m/s on a rough horizontal surface with coefficient of friction 0.2 . Given, g=10ms2 ,the time after which the sphere stops slipping (in seconds) is
Step by step video & image solution for A uniform sphere is projected horizontally with a purely translatory motion with initial velocity of 7m/s on a rough horizontal surface with coefficient of friction 0.2 . Given, g=10m/s^(2) ,the time after which the sphere stops slipping (in seconds) is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
View SolutionA body is projected horizontally from a height of 78.4m with a velocity 10m/s .Its velocity after 3 seconds is ?[g=10m/ s^(2) ]
View Solution500 g द्रव्यमान का एक पिंड एक खुरदरे क्षैतिज मेज पर फिसलता है यदि पिण्ड तथा मेज के मध्य गुणांक 0.2 है तथा पिण्ड की प्रारम्भिक चाल60cm/s है । तब
वह समय इस पर यह रुकता है यदि t = 0 पर पिण्ड का वेग 60 cm/s है
View SolutionA body of mass 10 kg moves on rough horizontal surface with initial velocity 10m/s and travels 500m before coming to rest. The coefficient of friction is
View SolutionA disc of mass m and radius R is given a linear velocity V_(0) on a rough horizontal surface. Initially the motion of the disc is purely translatory. The work done by friction in changing the motion of the disc from pure translatory to pure rolling is 1/xmv_(0)^(2) where 'x' is
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface the maximum value of F so that sphere will not slip is equal to (friction coefficient= mu )
View SolutionA block is projected with speed 20 m/s on a rough horizontal surface. The coefficient of friction (μ) between the surface varies with time (t) as shown in figure. The speed of body at the end of 4 second will be (g=10m/s2)
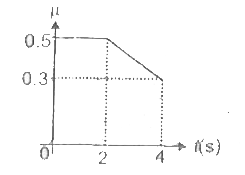
View Solution
