Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ΔV(<<V) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P1 to P2 ?Solution in Gujrati
The pressure is increased by ΔP, when volume is increased by ΔV at each stroke.
∴P1Vγ1=P2Vγ2 (Initially)
∴P(V+ΔV)γ=(P+ΔP)Vγ (∵ volume is fixed )
PVγ[1+ΔVV]γ=P[1+ΔPP]Vγ
As ΔV<<V so by using binomial theorem we get ,
∴PVγ(1+γΔVV)=PVγ(1+ΔPP)
∴γΔVV=ΔPP
∴ΔV=1γ.VP.ΔP
But ΔV and ΔP are very small.
dV=1γ.VP.dP
Hence, work done in increasing the pressure in tube from P1 to P2 is
W=∫P2P1PdV=∫P2P1P×1γ×VP.dP
=Vγ∫P2P1dP
=Vγ(P2−P1)
∴W=(P2−P1)Vγ
Topper's Solved these Questions
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-D Ncert Exemplar Solution (Long Answer )
Explore 5 Videos
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-E MCQs
Explore 42 Videos
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Section-D Ncert Exemplar Solution (Very Short Answer )
Explore 5 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
- UNITS AND MEASUREMENTBook:KUMAR PRAKASHANChapter:UNITS AND MEASUREMENTExercise:Section -F (Questions from Module )
Explore 20 Videos
Similar Questions
Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in figure.

(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperature T1T2 if V2=2V1 ?
(c) Given the internal energy for one mole of gas at temperature T is 32RT, find the heat 2 supplied to the gas when it is taken from state 1 to 2, with V2=2V1
View SolutionHeat absorbed by the gas undergo a cylic process along closed path in one complete cycle as shown in figure will be _____ J.
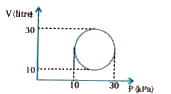
View SolutionCan a system be heated and its temperature remains constant ?
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionIf the error in measurement of radius of a shpere is 2% then the error in determination of volume of the sphere will be …………
View SolutionConsider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump DeltaV(lt lt V) of air is transferred to the tube adiabatically . What is the work done when the pressure in the tube is increased from P_(1) to P_(2) ?
View SolutionWhen air is pumped into a cycle tyre, the volume and pressure of the air in the tyre, both are increased.
What about Boyle's law in this case?
View SolutionWhen air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Bouyle's law in this case?
View SolutionConsider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump DeltaV(ltltV) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from p_(1) to p_(2) ?
View SolutionWhen air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle's law in this case?
View SolutionWhen air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle's law in this case?
View SolutionThe tyre of a motorcar bursts suddenly when air was being pumped in it. The internal pressure became 3 times the atmospheric pressure during pumping. If the initial temperature of the air inside the tyre is 27^(@)C , what will be the decrease in temperature of air due to the bursting of tyre? for air, gamma = 1.4 .
View SolutionAir is being pumped into the tyre of a car at a specific pressure. When the pressure of the tyre become double and the temperature of air is 15∘C, the tyre bursts suddenly. Find out the change in temperature.
View SolutionWe often have the experience of pumping air into bicycle tyre using hand pump. Consider the air inside the pump as a thermodynamic system having volume V at atmospheric pressure and room temperature, 27^(@)C . Assume that the nozzle of the tyre is blocked and you push the pump to a volume 1//4 of V. Calculate the final temperature of air in the pump? (For air, since the nozzle is blocked air will not flow into tyre and it can be treated as an adiabatic compression). Take gamma for air = 1.4
View SolutionWhen air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Bouyle's law in this case?
View Solution