A conducting bar of 3m length is allowed to fall freely from 80m high tower, keeping it aligned along the East-West direction. Find the emf induced in the rod when it is 20m below the top of tower.
g=10ms−2,Bh=0.7×10−4T and angle of deep = 60∘ . Solution in Gujrati
2.5 mV
2.1 mV
2.7 mV
1.2 mV
The correct Answer is:B
Here l=3 m
h=80 m
d=20 m
g=10ms−2
Bh=0.7×10−4T
ϕ=60∘
Put v0=0 in kinetic equation v2−v20=2gd
∴v2=2gd
∴v2=2×10×20
∴v2=400
∴ v=20 m/s
⇒ Kinetic emf
E=Bvl
=Bhcosϕvl
=0.7×10−4×cos60∘×20×3
=0.7×10−4×12×20×3
=2.1×10−3 V
∴ E=2.1 mV
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D MCQs (MCQs asked in Competitive Exams )
Explore 38 Videos
- ELECTROMAGNETIC INDUCTIONBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC INDUCTIONExercise:Section C Ncert Exemplar Solution (Long Answer )
Explore 11 Videos
- ELECTRIC CHARGES AND FIELDS Book:KUMAR PRAKASHANChapter:ELECTRIC CHARGES AND FIELDS Exercise:SECTION D MCQS ASKED IN COMPETITIVE EXAMES (MCQS AKSED IN BOARD EXAM AND GUJCET)
Explore 14 Videos
- ELECTROMAGNETIC WAVESBook:KUMAR PRAKASHANChapter:ELECTROMAGNETIC WAVESExercise:BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
Explore 5 Videos
Similar Questions
Three pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionA magnetic field →B=B0sin(ωt)ˆk covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d as in figure. The wires are in the xy-plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity ?
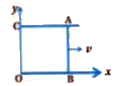
View SolutionWhen air is replaced by dielectric medium of constant K, the maximum force of attraction between two charges separated by distance d, ..........
View SolutionDetermine the current in each branch of the given network.

View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.
View Solution7 मीटर ऊँची एक इमारत के शीर्ष से, एक केबल टॉवर के शीर्ष पर उन्नयन कोण 60∘ है| तथा टॉवर के पाद पर अवनमन कोण 30∘ है|टॉवर की ऊंचाई ज्ञात कीजिए|
View Solution7 m ऊँचे एक भवन के शीर्ष से किसी मीनार के शीर्ष का उन्यनन कोण 60∘ है और मीनार के चरण का अवनति कोण 30∘ है| मीनार की ऊंचाई ज्ञात कीजिए|
View SolutionFrom a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20m high building are 45∘ and 60∘ respectively. Find the height of the tower.
View SolutionFrom the top of a 10 m high building, the angle of elevation of the top of a tower is 60∘ and the angle of depression of its foot is 45∘. Find the height of the tower
View SolutionFrom the top of a cliff, 200m high, the angle of depression of the top and bottom of a tower are observed to be 30∘ and 60∘, find the height of the tower.
View SolutionAngle of elevation of the top of the tower from station A to the west of a tower 45^(@) is. Station B, located 10 meters from A, to the south of the east of the tower 45^(@) Angle of elevation of the top of the tower from 30^(@) Is the height of the tower
View SolutionA conducting bar of 2m length is allowed to fall freely from a 50m high tower, keeping it aligned along the east-west direction. Find the emf induced in the rod when it is 20 m below the top of the tower. g=10ms−2. Horizontal component of earth's magnetic field is 0.7×10−4 T and angle of dip =60∘.
View SolutionWhen a metallic rod falls freely, keeping its length horizontal and parallel to north-south direction, emf induced across it is ______
View SolutionAn object fallen freely from top of tower reaches at ground in 4s, then find the height of tower. (Take g=10ms−2)
View SolutionFrom the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.
View Solution

