A conservative force, , where is in meters, acts on a particle moving along an axis. The potential energy U associated with this force is assigned a value of 27 J at . (a) Write an expression for U as a function of , with U in joules and in meters. (b) What is the maximum positive potential energy ? At what (c) negative value and (d) positive value of is the potential energy equal to zero ?
The correct Answer is:(a) .
Step by step video, text & image solution for A conservative force, vec(F)=(6.0x-12)hat(i)N, where x is in meters, acts on a particle moving along an x axis. The potential energy U associated with this force is assigned a value of 27 J at x=0. (a) Write an expression for U as a function of x, with U in joules and x in meters. (b) What is the maximum positive potential energy ? At what (c) negative value and (d) positive value of x is the potential energy equal to zero ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
The potential energy of a particle of mass 2kg moving along the x-axis is given by U(x)=4x2−2x3( where U is in joules and x is in meters). The kinetic energy of the particle is maximum at
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View Solution
Knowledge Check
A single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
Determine the equation of F(x) as a function of x.A(a) F=2+xB(b) F=2+3xC(c) F=2(2−x)D(d) F=3+2xA particle of mass 4 kg moves along x axis, potential energy ( U ) varies with respect to x as U=20+(x−4)2 , maximum speed of paritcle is at
Ax=4Bx=2Cx=0Dx=2.5A single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
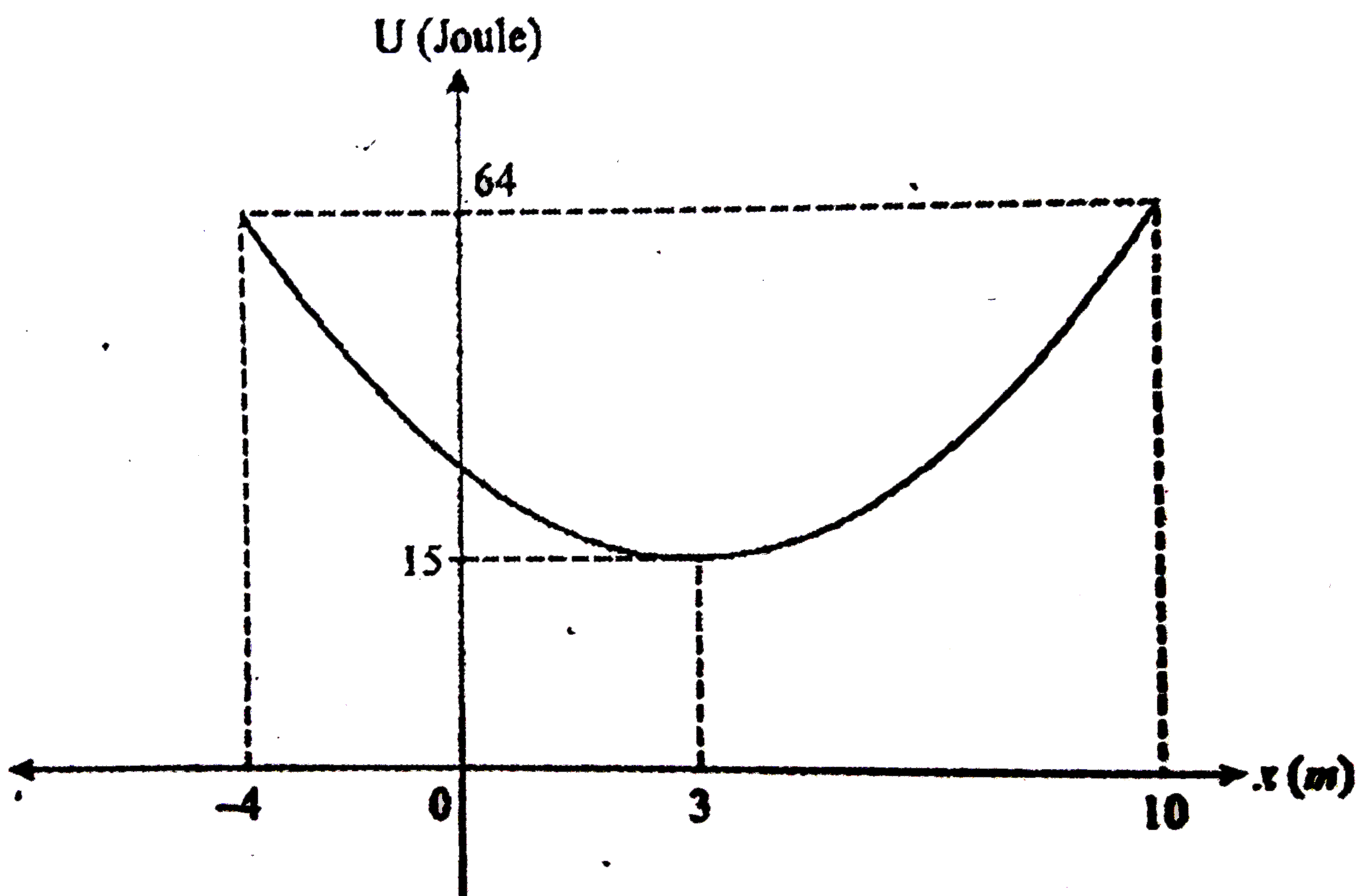 AThe mechanical energy of system is 69 JBThe mechanical energy of system is 19 JCAt x=3 the kinetic energy of particle is minimumDThe maximum value of kinetic energy is 54 J
AThe mechanical energy of system is 69 JBThe mechanical energy of system is 19 JCAt x=3 the kinetic energy of particle is minimumDThe maximum value of kinetic energy is 54 J
A single conservative force F(x) acts on particle that moves along the x-axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energyof 50J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule, where x is in mete then :
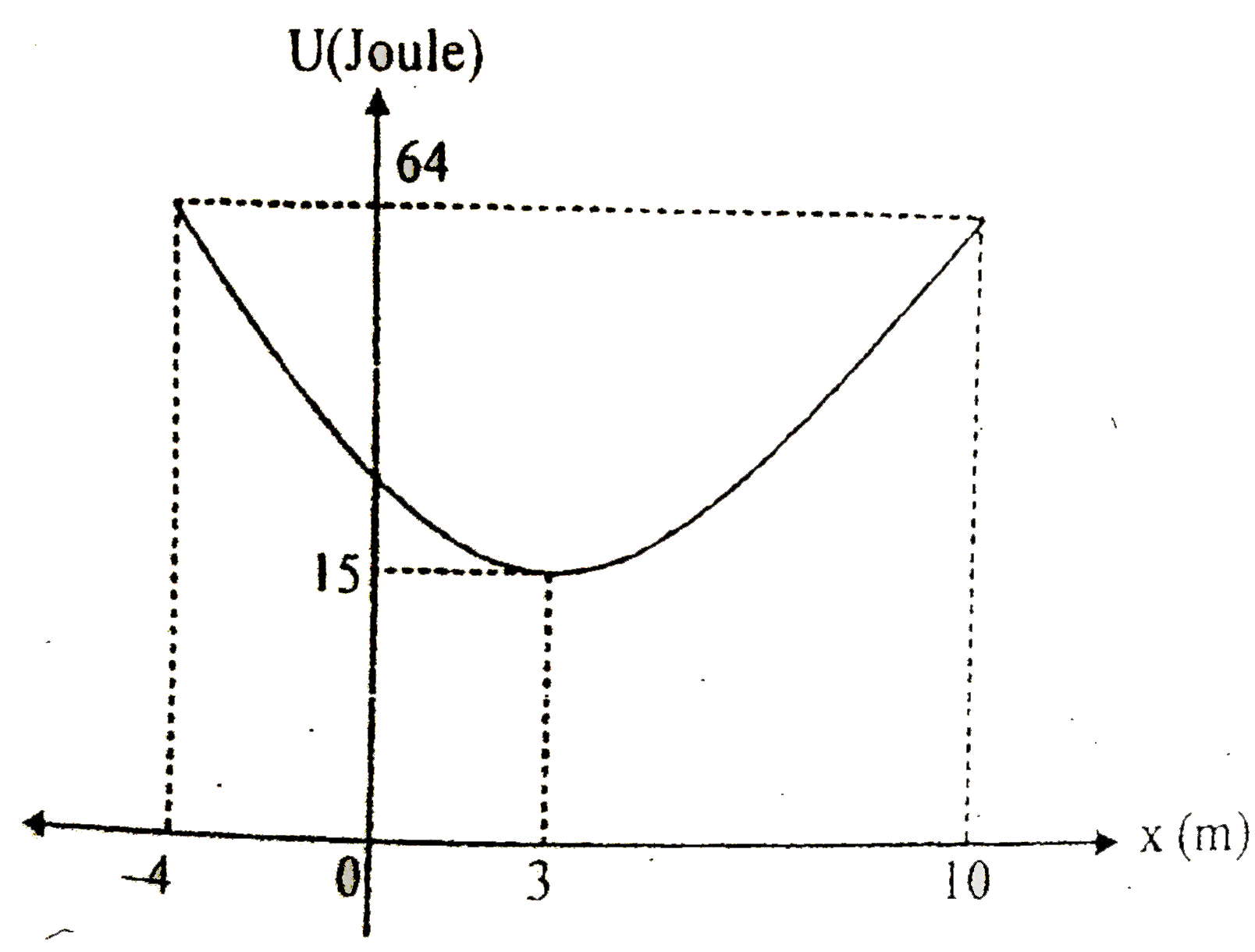
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The largest value of x will be:
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum speed of the particle is:
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, are
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
What is the mechanical energy of a system?
View Solution
