A 1.0 kg block is initially at rest on a horizontal frictionless surface when a horizontal force along an x axis is applied to the block. The force is given by →F(x)=(2.5−x2)ˆiN, where x is in meters and the initial position of the block is x=0. (a) What is the kinetic energy of the block as it passes through x=2.0m ? (b) What is the maximum kinetic energy of the block between x=0 and x=2.0m ?
The correct Answer is:(a) 2.3 J; (b) 2.6 J
To solve the problem, we will use the work-energy theorem, which states that the work done on an object is equal to the change in its kinetic energy. Let's break down the solution step by step.
1. Calculate the Work Done from x=0 to x=2:
The work done W is given by the integral of force over the displacement:
W=∫20F(x)dx=∫20(2.5−x2)dx
2. Evaluate the Integral:
W=∫20(2.5−x2)dx=(2.5x−x33)20
- At x=2:
W=2.5(2)−(2)33=5−83=5−2.67=2.33J
3. Apply the Work-Energy Theorem:
Since the block starts from rest, its initial kinetic energy KE0=0:
W=KEf−KE0⟹KEf=W
Therefore, the kinetic energy at x=2:
KE=2.33J
Part (b): Maximum Kinetic Energy between x=0 and x=2
1. Find the Expression for Kinetic Energy:
From part (a), we have:
KE(x)=2.5x−x33
2. Differentiate to Find Critical Points:
To find the maximum kinetic energy, we differentiate KE(x) with respect to x and set it to zero:
d(KE)dx=2.5−x2=0
Solving for x:
x2=2.5⟹x=√2.5≈1.58m
3. Check if x=√2.5 is within the interval (0, 2):
Yes, 1.58m is within the interval.
4. Calculate the Kinetic Energy at x=√2.5:
Substitute x=√2.5 into the kinetic energy expression:
KE(√2.5)=2.5(√2.5)−(√2.5)33
- Calculate KE:
KE(√2.5)=2.5⋅√2.5−(2.5)3/23
=2.5⋅1.58−(2.5)⋅1.583≈3.95−1.32≈2.63J
Final Answers:
- (a) Kinetic energy at x=2.0m is approximately 2.33J.
- (b) Maximum kinetic energy between x=0 and x=2 is approximately 2.63J.
The work done W is given by the integral of force over the displacement:
W=∫20F(x)dx=∫20(2.5−x2)dx
W=∫20(2.5−x2)dx=(2.5x−x33)20
- At x=2:
W=2.5(2)−(2)33=5−83=5−2.67=2.33J
Since the block starts from rest, its initial kinetic energy KE0=0:
W=KEf−KE0⟹KEf=W
Therefore, the kinetic energy at x=2:
KE=2.33J
From part (a), we have:
KE(x)=2.5x−x33
To find the maximum kinetic energy, we differentiate KE(x) with respect to x and set it to zero:
d(KE)dx=2.5−x2=0
Solving for x:
x2=2.5⟹x=√2.5≈1.58m
Yes, 1.58m is within the interval.
Substitute x=√2.5 into the kinetic energy expression:
KE(√2.5)=2.5(√2.5)−(√2.5)33
- Calculate KE:
KE(√2.5)=2.5⋅√2.5−(2.5)3/23
=2.5⋅1.58−(2.5)⋅1.583≈3.95−1.32≈2.63J
- (a) Kinetic energy at x=2.0m is approximately 2.33J.
- (b) Maximum kinetic energy between x=0 and x=2 is approximately 2.63J.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of an axis is applied to the block. The force is given by →F=(1−x2)ˆiN, where x is in meters and the initial position of the block is x=0 the maximum kinetic energy of the block is 2nJ in between x=0 ad x=2m find the value of n.
View SolutionIn Fig 15.5, the block has a kinetic energy of 3J and the spring has an elastic potential energy of 2J when the block is at x=+2.0cm. (a) What is the kinetic energy when the block is at x= 0? What is the elastic potential energy when the block is at (b) x=−2.0cm and (c ) x=−xm?
View Solution
Knowledge Check
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum positive displacement x isA(a) 2√3B(b) 2mC(c) 4mD(d) √2mA 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m isA(a) 2.33JB(b) 8.67JC(c) 5.33JD(d) 6.67JA 1.5kg block is initially at rest on a horizontal frictionless surface. A horizontal force →F=(4−x2)ˆi is applied on the block. Initial position of the block is at x=0. The maximum kinetic enery of the block between x=0 and x=2m is
A2.33JB8.67JC5.33JD6.67J
Blocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
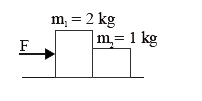
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View SolutionBlocks are in contact on a frictionless table. A horizontal force F = 3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is-
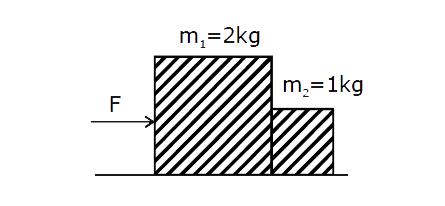
View SolutionA block of mass 4kg is initially at rest on a horizontal frixtionless surface. A horizontal force →F=(3+x)ˆi newtons acts on it, when the block is at x=0. The maximum kinetic energy of the block between x=0 and x=2m is
View SolutionA block of mass 2 kg, initially at rest on a horizontal floor, is now acted upon by a horizontal force of 10N. The coefficient of friction between the block and the floor is 0.2. If g=10m/s2, then :
View Solution
