A ball is thrown from the top of a tower of 67 m high with a velocity 24.4ms−1 at an clevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
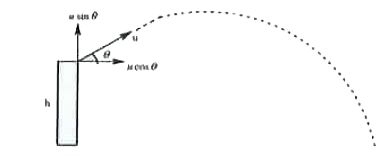
h=12gt2−(−usinθ)t ⇒t=5 sec onds
Also, d=(ucosθt=105.65m)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)25videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)10videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - PROBLEMS (LEVEL-II)13videos
MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER7videos
MOTION IN A PLANE
Similar Questions
A ball is thrown from the top of a tower of 61m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
View SolutionA ball is throw from the top of a tower of 61 m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizon. What is the distance from the foot of the tower to the point where the ball hits the ground ?
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown from the top of tower with an initial velocity of 10ms−1 at an angle of 30∘ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is (Takeg=10ms−2)
A5mB20mC15mD10m - Question 2 - Select One
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m - Question 3 - Select One
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
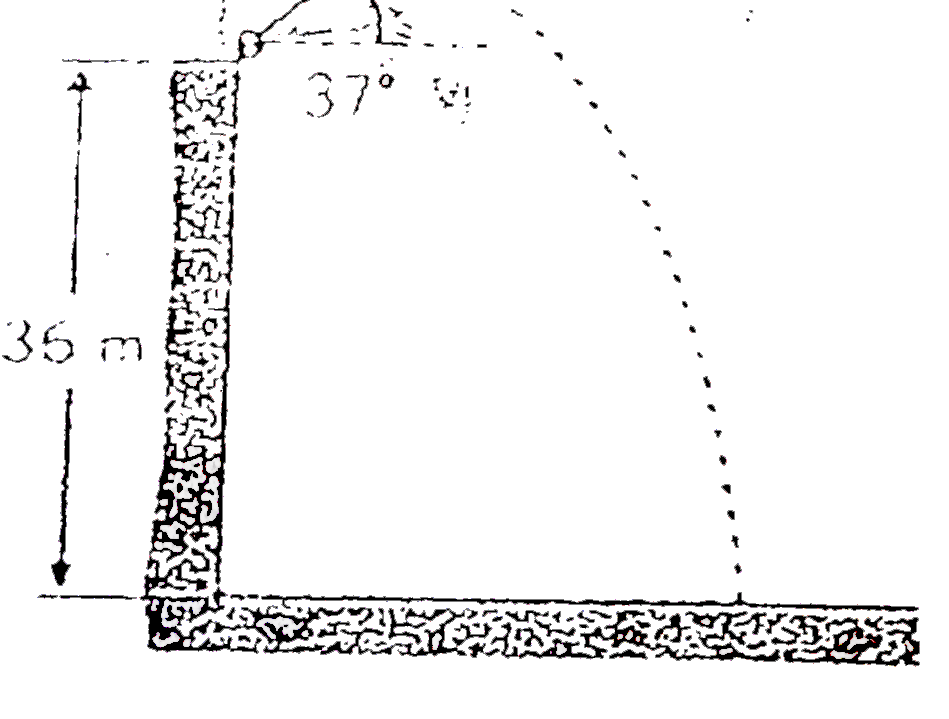: A12mB18mC24mD30m
A stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
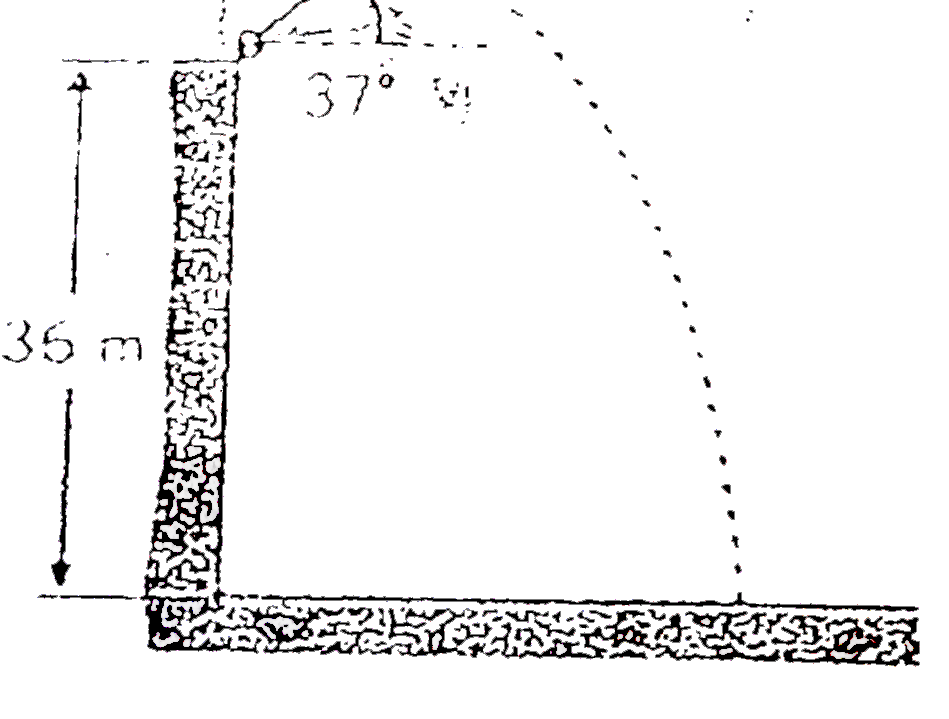: View SolutionA ball is thrown with a velocity of 30ms−1 from the top of a building 200m high . The ball makes an angle of 30∘ with the horizontal . Calculate the distance from the foot of the building where the ball strikes the ground (g=10ms−2).
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View Solution