दो सदिशों का परिमाण समान है जिसका मान F है। यदि बराबर है
इनमें से कोई नहीं
The correct Answer is:A
या
Topper's Solved these Questions
Similar Questions
दिया है, C=A×B तथा D=B×AI C तथा D के बीच कोण क्या है?
View Solutionएक डायोड की धारा वोल्टता संबंध I=(e1000V/T−1) मिली ऐम्पियर दिया गया है । जहां लगाई वोल्टता V वोल्ट में है और तापमान T केल्विन में है। यदि एक विद्यार्थी 300 K पर 5 मिली ऐेम्पियर धारा मापते समय ±0.01 V की त्रुटि करता है तब धारा के मान में मिली ऐम्पियर में होने वाली त्रुटि क्या होगी?
View SolutionGiven examples of two one-one functions f1andf2 from R to R such that f1+f2:R→R, defined by (f1+f2)(x)=f1(x)+f2(x) is not one-one.
View SolutionLet f1:R→Randf2:C→C are two functions such that f1(x)=x3andf2=x3.Prove that f1andf2are not same.
View SolutionGive examples of two one-one functions f1 and f2 from R to R such that f1+f2:R→R , defined by (f1+f2)(x)=f1(x)+f2(x) is not one-one.
View SolutionShow that if f1 and f2 are one-one maps from R to R , then the product f1×f2:R→R defined by (f1×f2)(x)=f1(x)f2(x) need not be one-one.
View SolutionTwo forces F_(1) and F_(2) are acting at a point, whose resultant is F .If F_(2) is doubled F is also doubled. If F_(2) is reversed then also F is doubled. Then F_(1):F_(2):F is
View SolutionIf F1andF2 aare two vectors of equal magniudes F such that |F1.F2|=|F1×F2|,then|F1+F2| equals to
View SolutionLet f1(x)andf2(x) be twice differentiable functions where F(x)=f1(x)+f2(x)andG(x)=f1(x)−f2(x),∀x∈R,f1(0)=2andf2(0)=1.Iff'1(x)=f2(x)andf'2(x)=f1(x),∀x∈R. then the number of solutions of the equation (F(x))2=9x4G(x)is...... .
View SolutionFor the following table, the values of f1, f0 and f2 are respectively______.
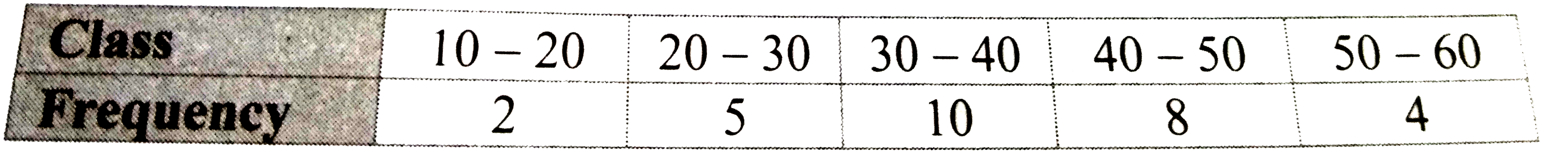
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F5 is
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F3 is ____.
View SolutionThe correct relation between magnitude of f1 and f2 in above problem is :
(A) f1>f2 (B) f2>f1 (C )f1=f2 ( D) not possible to decide due to insufficient data.
View Solutionl+(f1−f02f1−f0−f2)×hसूत्र है:
View Solutionf1(x)=x+a,f2(x)=x2+bx+c and Δ=∣∣ ∣ ∣∣111f1(x1)f1(x2)f1(x3)f2(x1)f2(x2)f2(x3)∣∣ ∣ ∣∣, then Δ is independent of
View Solution
