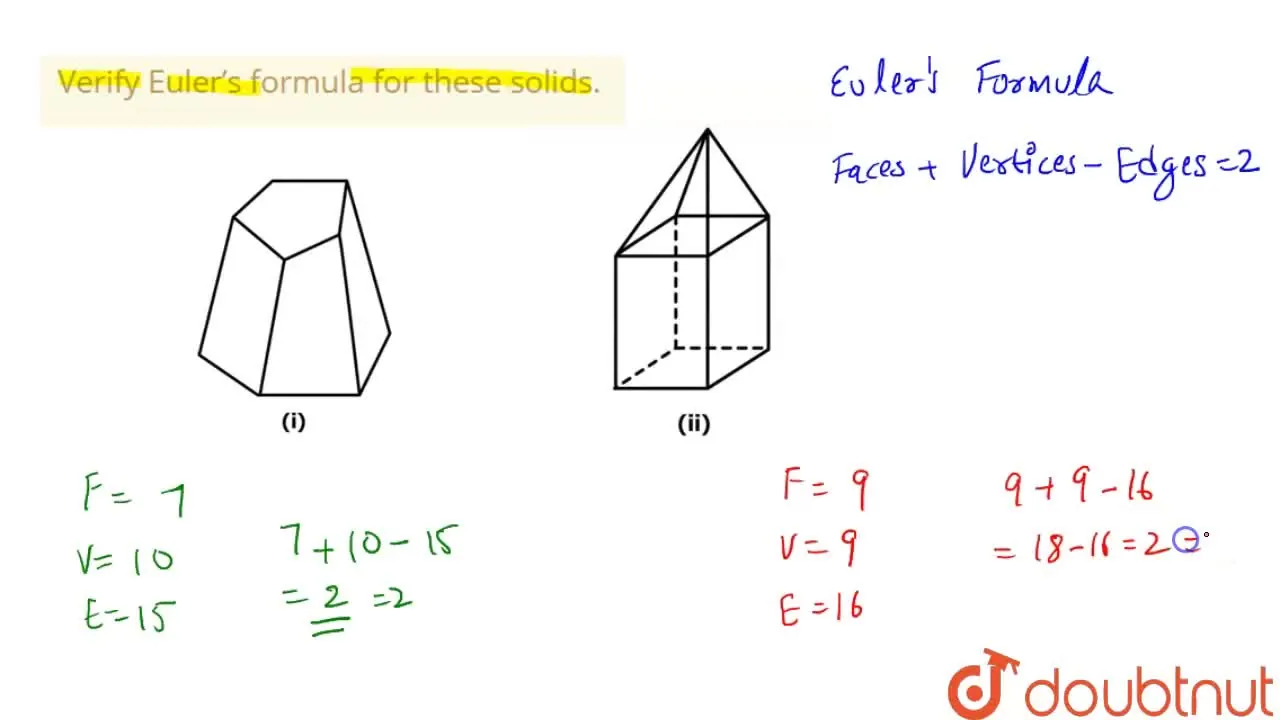
Verify Euler’s formula for these solids.
The correct Answer is:Eulers formula
Face + Vertices - Edges = 2
(1)Face=7
Vertices=10
Edges=15
Eulers = F+V−E=7+10−15=2
(2) Face=9
Vertices=9
Edges=16
Eulers = F+V−E=9+9−16=2.
Eulers formula
Face + Vertices - Edges = 2
(1)Face=7
Vertices=10
Edges=15
Eulers = F+V−E=7+10−15=2
(2) Face=9
Vertices=9
Edges=16
Eulers = F+V−E=9+9−16=2.
Related Playlists
Similar Questions
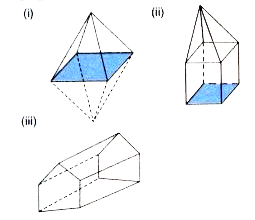
Verify Euler's formula for the following three dimensional figures :
 View Solution
View SolutionVerify Euler’s formula for each of the following polyhedrons: Figure (ii) Figure (iii) Figure
View SolutionComplete the following table and verify Euler’s formula in each case.
View SolutionWhat is the Euler’s formula for a Polyhedron?
View SolutionUsing Euler’s formula find the unknown. Faces ?,5,20 , vectices 6,?,12 and Edges 12,9,?
View SolutionA binary solid A+B− has a structure with B− ions constituting the lattice and A+ ions occupying 25% tetrahedral holes. Formula of the solid is
View SolutionA solid is formed and it has three types of atoms X, Y, Z. X forms an FCC lattice with Y atoms occupying one-fourth of tetrahedral voids and Z atoms occupying half of the octahedral voids. The formula of the solid is
View SolutionUsing Euler’s formula find the unknown: Faces, ?, 5, 20 Vertices, 6, ?, 12 Edges, 12, 9, ?
View SolutionUse Euler's formula to find the values of a, b and c.
 View Solution
View SolutionUsing Euler's formula, find the values of x, y and z
 View Solution
View Solution