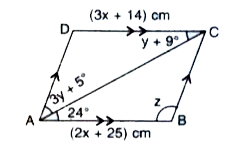
Consider the following parallelograms. Find the values of the unknowns x, y, z.
(i)Since D is opposite to B.
So,
(Since oppositeanglesofparallelogram areequal)
(The adjacent angles in a parallelogram are supplementary
Therefore
[Since opposite angles of a parallelogram are equal]and adjacent angles are supplementary.]
Using this property, we cancalculate the measure of the unknown angles.]
Solution:]
(The adjacent angles in aparallelogramaresupplementary )]
(Since opposite angles of a parallelogram are equal)
(Corresponding angle
(iii)In a parallelogram, opposite angles are equal
and adjacent angles are supplementary.Using this property,
wecancalculate the measure of the unknown angles.
Solution
(Corresponding angles)
(since oppositeanglesofaparallelogramareequal
(Adjacentanglesaresupplementary
therefore
,,
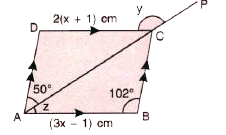
(iv)In a parallelogram, opposite angles are equal and adjacent angles are
supplementary.
Using this property, we can
calculate the measure of the unknown angles.
(angle sum property of triangle)
(vertically opposite angles
(alternate interior angle)
(v )
(Alternate interior angle)
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.49videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
The following figures are parallelograms. Find the degree values of the unknowns x, y, z figure (ii) figure (iii) figure figure (v) figure (vi) figure
View SolutionFind the value of x, y and z
View SolutionFind the value of x, y and z
View SolutionFind the value of x,y and z.
View SolutionUse the information given in the following diagram to find the values of x, y and z.
 .View Solution
.View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
 View Solution
View SolutionIn Fig 3.26, BEST is a parallelogram. Find the values x, y and z.
View SolutionIf the points (−2, −1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y .
View SolutionIn Figure, BEST is a parallelogram. Find the values of x, y and z.
View SolutionConsider the following graph:

X, Y and Z can be respectivelyView Solution
