Can a quadrilateral ABCD be a parallelogram if (i) <D+<B=180∘ ? (ii) AB=DC=8cm,AD=4cmandBC=4.4cm ? (iii) A=70∘and<C=65∘ ?
(i) ∠D+∠B=1800
The sum of measure of adjacent angles in a paralellogram should be 1800, hence it may or may not be possible.
(ii) AB=DC=8cm,AD=4cmandBC=4.4cm
This is not possible, as opposite sides must be of same length for a paralleogram to exist.
(iii) ∠A=700and∠C=650
This is not possible, as opposite angles should be of equal.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.49videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
Is quadrilateral ABCD a parallelogram?
I. Its opposite sides are equal.
II. Its opposite angles are equal.
The correct answer is : (a) /(b)/(c )/(d).Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together. - Question 2 - Select One
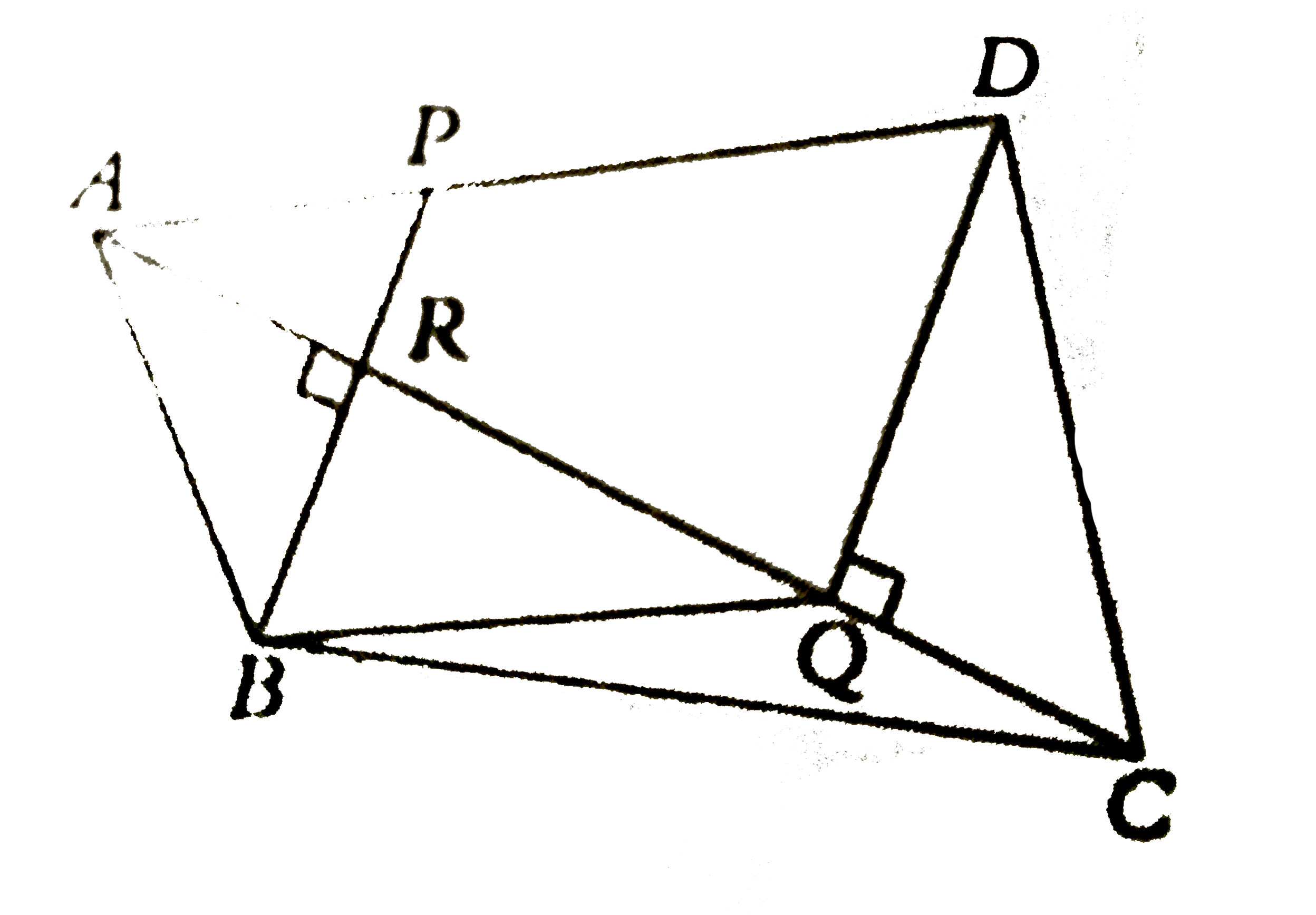
In the figure given above, ABCD is a quadrilateral and BPDQ is parallelogram. AR = 50 cm, CQ = 70 cm, BR = 60, and PR = 40 cm. If the area of the quadrilateral ABCD is 15,600cm2, then find the area of then find the area of the parallelogram BPDQ (in cm2).A9460B8460C7500D9000 - Question 3 - Select One
Which of the following quadrilateral is not a parallelogram ?
ARectangleBSquareCRhombusDNone of these
Given statements . Identify the statements given below as contrapositive or converse of each other.
If a quadrilateral is a parallelogram, then its diagonals bisect each other.
(i) If the diagonals of a quadrilateral do not bisect each other, then the quadrilateral is not a parallelogram.
(ii) If the diagronals of a quadrilateral bisect each other, then it is a parallelogram.View SolutionIf the diagonals AC, BD of a quadrilateral ABCD, intersect at O, and separate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram.
View SolutionThe converse of the above properties are also true i.e.(i) A quadrilateral is a parallelogram if its opposite sides are equal.(ii)A quadrilateral is a parallelogram if its opposite angles are equal.(iii) A quadrilateral is a parallelogram if it has one pair of opposite sides parallel and equal.(iv) A quadrilateral is a parallelogram if its diagonals bisect each other .
View SolutionWhich of the following statements are true (T) and which are false (F)? (i) In a parallelogram, the diagonals are equal. (ii) In a parallelogram, the diagonals bisect each other. (iii) In a parallelogram, the diagonals intersect each other at right angles. (iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram. (v) If all the angles of a quadrilateral are equal, it is a parallelogram. (vi) If three sides of a quadrilateral are equal , it is a parallelogram. (vii) If three angles of a quadrilateral are equal, it is a parallelogram. (viii) If all the sides of a quadrilateral are equal it is a parallelogram
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC.IF∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate wach angle of the quadrilateral.
(ii) Assign special name to quadrilateral ABCD.View Solution