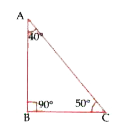
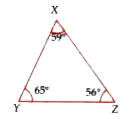
Name each of the following triangles in two different ways: (you may judge the nature of the angle by observation)
To name each of the given triangles in two different ways, we will analyze them based on their angles and sides. Here’s a step-by-step solution:
Step 1: Identify the properties of the triangles
- Angles: Determine if the angles are acute (less than 90°), right (equal to 90°), or obtuse (greater than 90°).
- Sides: Determine if the sides are equal (equilateral), two sides are equal (isosceles), or all sides are different (scalene).
Step 2: Analyze each triangle
Triangle A
1. Observation: Two sides are equal, and all angles are less than 90°.
2. Naming:
- Isosceles Triangle (because two sides are equal)
- Acute Triangle (because all angles are less than 90°)
Triangle B
1. Observation: One angle is 90°, and all sides are different.
2. Naming:
- Right Triangle (because one angle is 90°)
- Scalene Triangle (because all sides are different)
Triangle C
1. Observation: Two sides are equal, and one angle is greater than 90°.
2. Naming:
- Isosceles Triangle (because two sides are equal)
- Obtuse Triangle (because one angle is greater than 90°)
Triangle D
1. Observation: One angle is 90°, and two sides are equal.
2. Naming:
- Right Triangle (because one angle is 90°)
- Isosceles Triangle (because two sides are equal)
Triangle E
1. Observation: All sides are equal, and all angles are less than 90°.
2. Naming:
- Equilateral Triangle (because all sides are equal)
- Acute Triangle (because all angles are less than 90°)
Triangle F
1. Observation: All sides are different, and one angle is greater than 90°.
2. Naming:
- Scalene Triangle (because all sides are different)
- Obtuse Triangle (because one angle is greater than 90°)
Summary of Names for Each Triangle
- Triangle A: Isosceles Acute Triangle
- Triangle B: Right Scalene Triangle
- Triangle C: Isosceles Obtuse Triangle
- Triangle D: Right Isosceles Triangle
- Triangle E: Equilateral Acute Triangle
- Triangle F: Scalene Obtuse Triangle
- Angles: Determine if the angles are acute (less than 90°), right (equal to 90°), or obtuse (greater than 90°).
- Sides: Determine if the sides are equal (equilateral), two sides are equal (isosceles), or all sides are different (scalene).
1. Observation: Two sides are equal, and all angles are less than 90°.
2. Naming:
- Isosceles Triangle (because two sides are equal)
- Acute Triangle (because all angles are less than 90°)
1. Observation: One angle is 90°, and all sides are different.
2. Naming:
- Right Triangle (because one angle is 90°)
- Scalene Triangle (because all sides are different)
1. Observation: Two sides are equal, and one angle is greater than 90°.
2. Naming:
- Isosceles Triangle (because two sides are equal)
- Obtuse Triangle (because one angle is greater than 90°)
1. Observation: One angle is 90°, and two sides are equal.
2. Naming:
- Right Triangle (because one angle is 90°)
- Isosceles Triangle (because two sides are equal)
1. Observation: All sides are equal, and all angles are less than 90°.
2. Naming:
- Equilateral Triangle (because all sides are equal)
- Acute Triangle (because all angles are less than 90°)
1. Observation: All sides are different, and one angle is greater than 90°.
2. Naming:
- Scalene Triangle (because all sides are different)
- Obtuse Triangle (because one angle is greater than 90°)
- Triangle A: Isosceles Acute Triangle
- Triangle B: Right Scalene Triangle
- Triangle C: Isosceles Obtuse Triangle
- Triangle D: Right Isosceles Triangle
- Triangle E: Equilateral Acute Triangle
- Triangle F: Scalene Obtuse Triangle
Topper's Solved these Questions
- UNDERSTANDING ELEMENTARY SHAPESBook:NCERT ENGLISHChapter:UNDERSTANDING ELEMENTARY SHAPESExercise:EXERCISE 5.2
Explore 7 Videos
- UNDERSTANDING ELEMENTARY SHAPESBook:NCERT ENGLISHChapter:UNDERSTANDING ELEMENTARY SHAPESExercise:EXERCISE 5.8
Explore 5 Videos
- SYMMETRYBook:NCERT ENGLISHChapter:SYMMETRYExercise:EXERCISE 13.2
Explore 6 Videos
- WHOLE NUMBERSBook:NCERT ENGLISHChapter:WHOLE NUMBERSExercise:SOLVED EXAMPLES
Explore 7 Videos
Similar Questions
Knowledge Check
Name each of the following angles
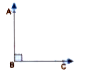 A∠BACB∠ABCC∠BCAD∠CAB
A∠BACB∠ABCC∠BCAD∠CABName each of the following angles
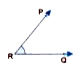 A∠QPRB∠RQPC∠RPQD∠PRQ
A∠QPRB∠RQPC∠RPQD∠PRQName each of the following angles
 A∠YXZB∠XYZC∠YZXD∠ZYX
A∠YXZB∠XYZC∠YZXD∠ZYX
Name the following triangle with regards to angles :
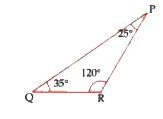
View SolutionIn each of the following figures, one side of a triangle has been produced. Find all the angles of the triangle in each case.
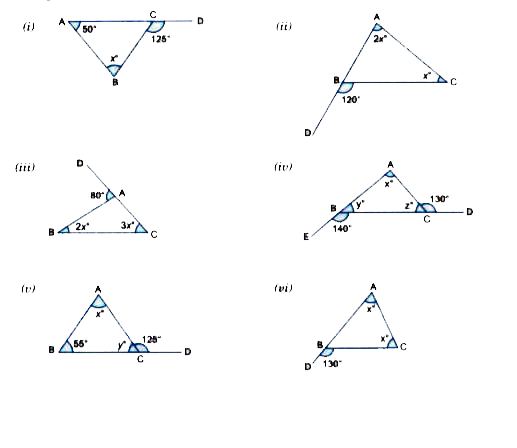
View SolutionEach of the two equal angles of a triangle is twice the third angle. Find the angles of the triangle.
View SolutionName any two source of e-wastes and write two different ways for their disposal.
View SolutionIn each of the following figures, you find two triangles. Indicate whether the triangles are similar. Give reasons in support of your answer. (FIGURES)
View Solution