A particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g = 10 m/s2)Solution in Telugu
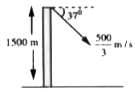
s=ut+12at2
1500=5003sin37+1210×t2
1500=5003×35t+5t2 300=20t+t2
On solving, t=10 s
∴ Horizontal distance =ucosθ, T
=5003×45×10=40003 m
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionIn the figures shown, three particles are thrown from a tower of height 40 m as shown in figure. In each case find the time when the particles strike the ground and the distance of this point from foot of the tower. , , .
View SolutionA particle is projected from a tower of height 25 m with velocity 20sqrt(2)m//s at 45^@ . Find the time when particle strikes with ground. The horizontal distance from the foot of tower where it strikes. Also find the velocity at the time of collision.
View SolutionA ball projected upwards from the foot of a tower. The ball crosses the top of the tower twice after an interval of 6s and the ball reaches the ground after 12s. The height of the tower is (g=10m/s2) :
View Solutiona shot is fired at an angle of 30∘ with horizontal from the top of a tower 182.88 metres high. The velocity of projection is 560.96m/s. Find where from the foot of tower it strikes the ground.
View SolutionA body thrown horizontally from the top of a building with a speed 20m/s, strikes the ground 40m away from the foot of tower. The height of the tower is
View SolutionA stone is projected at an angle alpha to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionA ball is projected from a point O as shown in figure. It will strike the ground after (g = 10 m//s^(2))
View SolutionA particle is thrown horizontally from a tower of height 20m . If the speed of projection is 20m/s then the distance of point from the tower,where the particle hit the ground is:-
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/ s^(2) )
View SolutionA body thrown horizontally from the top of a tower touches the ground at a distance of 160 m from the foot of the tower. If the velocity of projection is 40 m/s then the height of the towers is
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View Solution
