Question

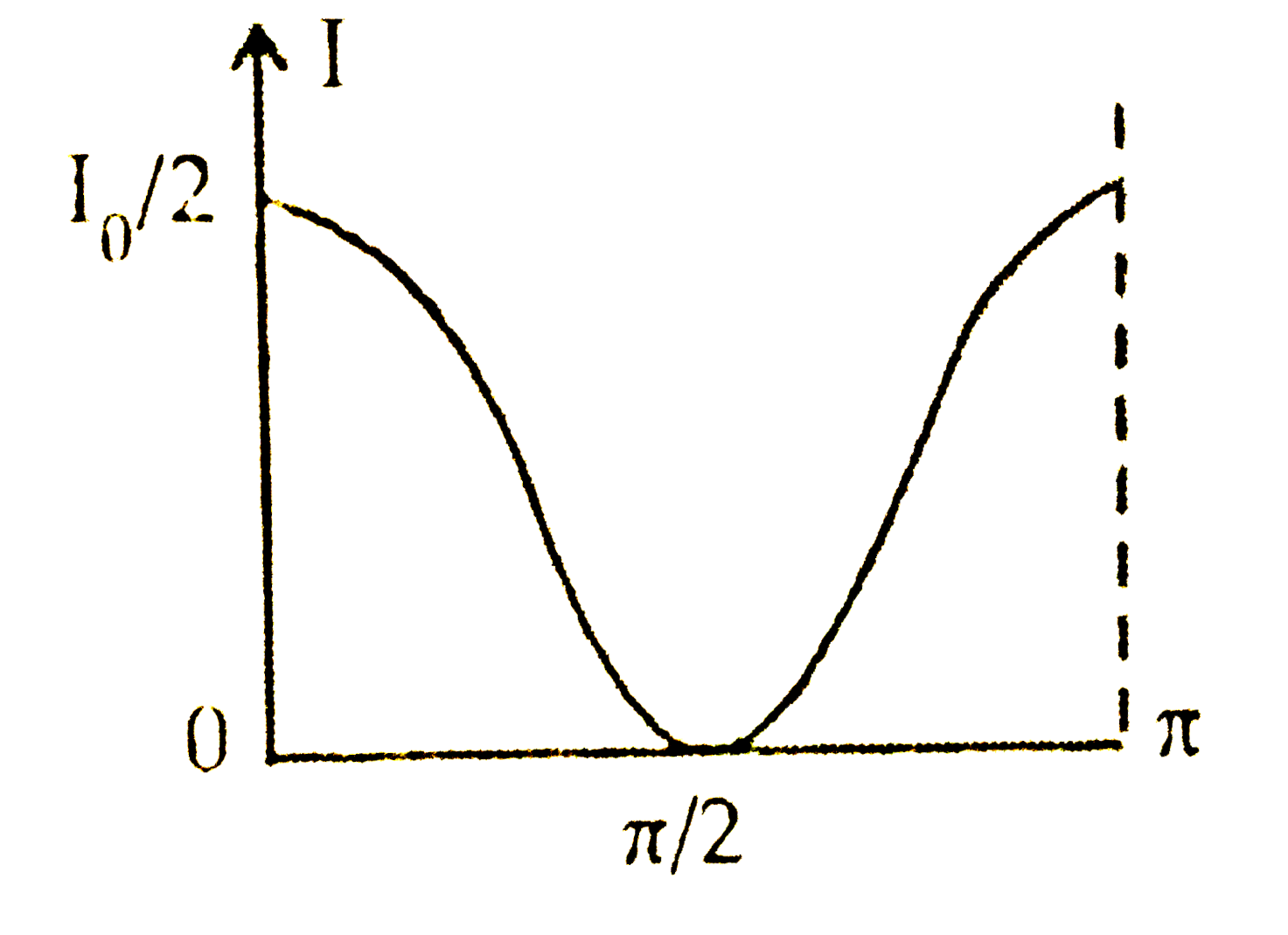
Unpolarised light is passed through a polaroid ${\displaystyle P_1}$. When this poalrised beam passes through another polaroid ${\displaystyle P_2}$, and if the pass axis of ${\displaystyle P_2}$ makes an angle ${\displaystyle \theta }$ with pass axis of ${\displaystyle P_1}$, then write the expression for the polarised beam passing through ${\displaystyle P_2}$. Draw a plot showing the variation of intensity when ${\displaystyle \theta }$ varies from 0 to 2 ${\displaystyle \pi }$.

Explanation

It is based on Law of Malus According to this law, when a completely polarised light is
incinent on an analyser , then the intensity of transmitted light varies directly as the
square of cosine of an angle between plane of polariser and plane of analyser.
`therefore I = I _(0) cos^(2) theta`
If the amplitude of transmitted light is a .
then, ` a = a_(0) cos^(theta) therefore a^(2) = a_(0) cos^(2) theta`
`therefore I = I _(0) cos^(2) theta rArr I alpha cos^(2) theta`
`therefore ` Veries from 0 to ` 2 pi and [ cos ^(2) theta] _(av) = (1)/(2pi) underset(0)overset(2) intcos ^(2) theta d theta`
`= (1)/(2pi) underset(0)overset(2pi) int(1 + cos ^(2) theta)/(2) d theta = (1)/(2pixx2) [0 + (sin2 theta)/(2)]^( 2pi) = (1)/(2) = I = I _(0) xx(1)/(2)`