A change q of mass m is moving with a velocity of V, at right angles to a uniform magnetic fiels B. Deduce the expression for the radius of the circular path it describes.
To derive the expression for the radius of the circular path described by a charged particle moving perpendicular to a uniform magnetic field, we can follow these steps:
1. Understanding the Forces Acting on the Charged Particle:
- A charged particle with charge q and mass m is moving with a velocity V at right angles to a uniform magnetic field B.
- The magnetic force acting on the charged particle is given by the Lorentz force equation:
F=q(V×B)
- Since the velocity V is perpendicular to the magnetic field B, the angle θ between them is 90∘. Thus, we can simplify the force to:
F=qVBsin(90∘)=qVB
2. Centripetal Force Requirement:
- As the charged particle moves in a circular path due to the magnetic force, this force acts as the centripetal force required to keep the particle in circular motion.
- The centripetal force Fc is given by:
Fc=mV2r
- Here, r is the radius of the circular path.
3. Setting the Forces Equal:
- Since the magnetic force provides the necessary centripetal force, we can set the two forces equal to each other:
qVB=mV2r
4. Rearranging the Equation:
- To find the radius r, we can rearrange the equation:
r=mV2qB
5. Final Expression:
- Thus, the expression for the radius r of the circular path described by the charged particle is:
r=mVqB
- A charged particle with charge q and mass m is moving with a velocity V at right angles to a uniform magnetic field B.
- The magnetic force acting on the charged particle is given by the Lorentz force equation:
F=q(V×B)
- Since the velocity V is perpendicular to the magnetic field B, the angle θ between them is 90∘. Thus, we can simplify the force to:
F=qVBsin(90∘)=qVB
- As the charged particle moves in a circular path due to the magnetic force, this force acts as the centripetal force required to keep the particle in circular motion.
- The centripetal force Fc is given by:
Fc=mV2r
- Here, r is the radius of the circular path.
- Since the magnetic force provides the necessary centripetal force, we can set the two forces equal to each other:
qVB=mV2r
- To find the radius r, we can rearrange the equation:
r=mV2qB
- Thus, the expression for the radius r of the circular path described by the charged particle is:
r=mVqB
Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SECTION-C
Explore 55 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
Explore 12 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SECTION-A
Explore 31 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B as shown in Find The radius of the circular are it describes in the magnetic field. (b) find the angle subtended by the arc at the centre. (c ) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.

View SolutionA particle of mass m and positive charge q,moving with a uniform velocity v enters a magnetic field B as shown in figure.(a) Find the radius of the circular arc it describes in the magnetic field. (b)Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d)Solve the three parts of the above problem if the charge q on the particle is negative.
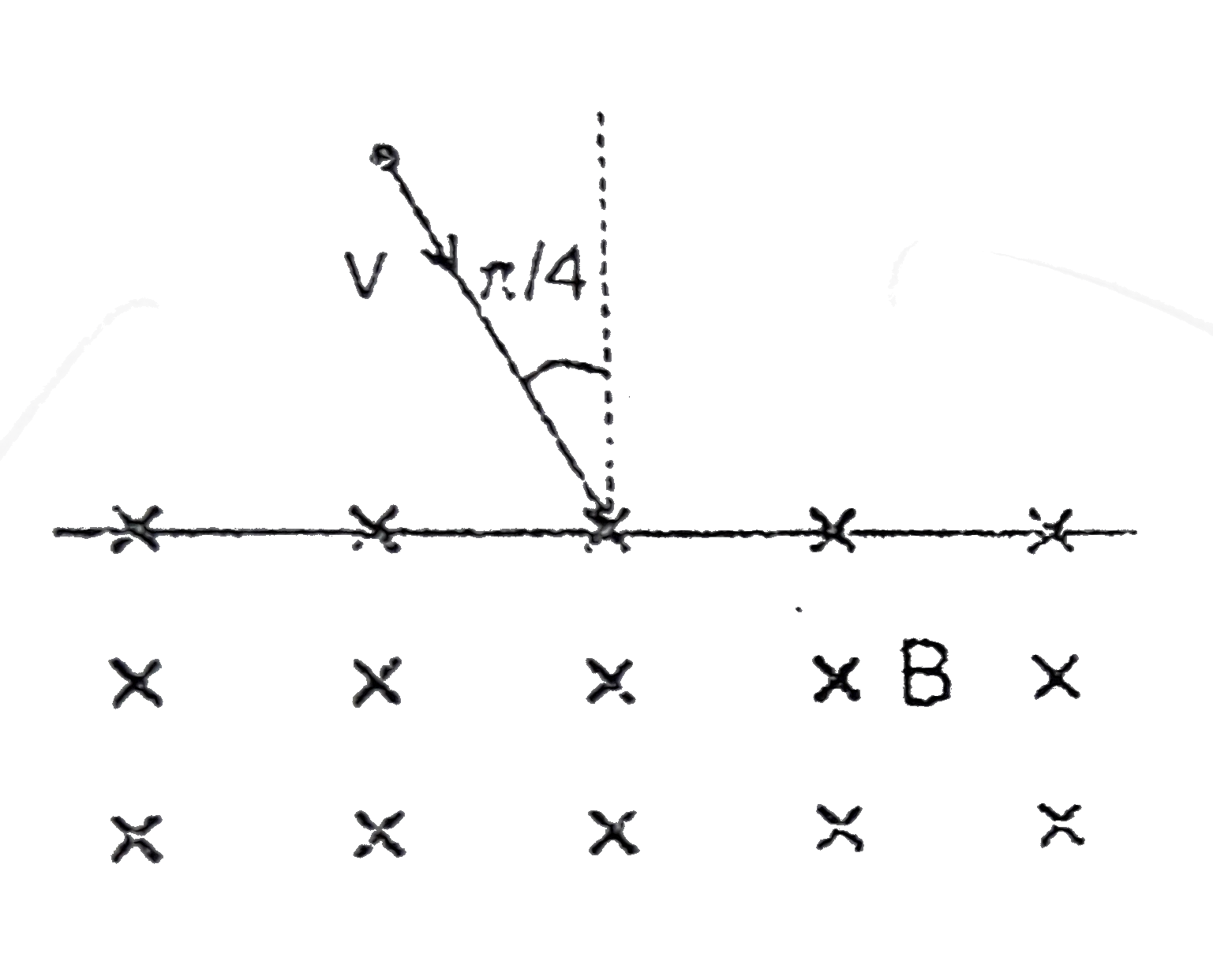
View Solution
Knowledge Check
An electron is moving in a circle of radius 'r' in a uniform magnetic field 'B'. Suddenly the field is reduced to 'B'2. The radius of the circular path now becomes
Ar2B2rCr4D4rAn electron of mass m and charge q is travelling with a speed v along a circular path of radius r at right angles to a uniform of magnetic field B. If speed of the electron is doubled and the magnetic field is halved, then resulting path would have a radius of
Ar4Br2C2rD4rA particle carrying a charge moves perpendicular to a uniform magnetic field of induction B with a momentum p then the radius of the circular path is
ABe/pBpe/BCp/BeDBep
A charged particle q moving in a straight line is accelerated by a potential difference V. It enters a uniform magnetic field B perpendicular to its path. Deduce in terms of V an expression for the radius of the circular path in which it travels.
View SolutionTwo particles having identical masses and charges 2Q and Q are moving with velocities v and 2v resp. In uniform magnetic field B. Find ratio of radius of circle described by them
View SolutionA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionIf a charge particle of charge q , mass m , moves in a circular path in magnetic field of induction B , under a potential of V volts then radius of circular path is
View Solution

