A long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
Field at outside points : The Amperean loop is a circle labelled 2 haveing radius r>a.
Length of the loop, L=2πr
Net current enclosed by the loop =I
By Ampere's circuital law,
BL=μ0I
or B×2πr=μ0I
or B=μ0I2πr
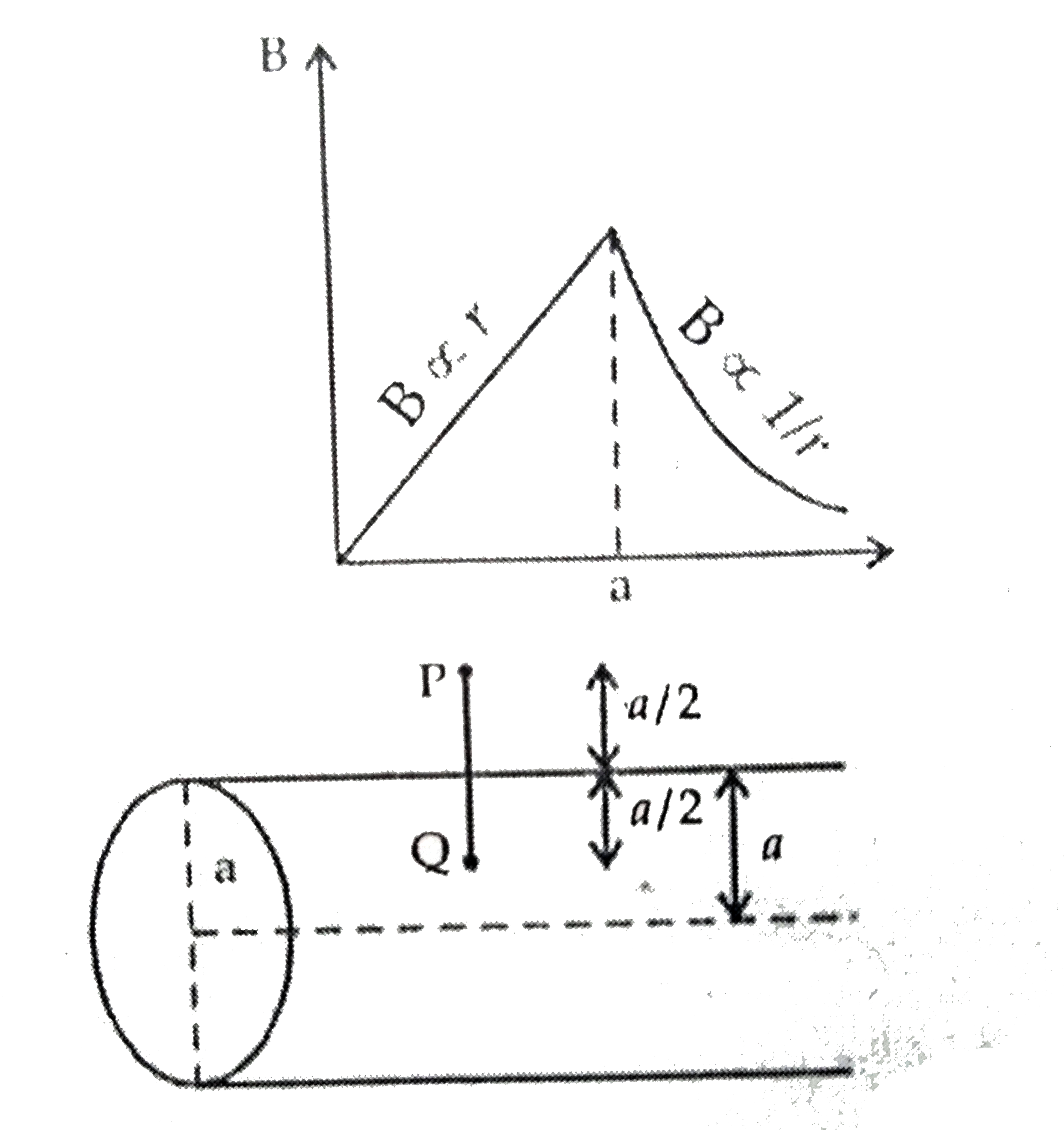
i.e., B∝1r [For outside points]
Field at inside points : The Amperean loop is a circle labelled 1 with r<a.
Length of the loop, L=2πr
So, the current enclosed by loop 1 is less than I. As the current distribution is uniform, the fraction of I enclosed is
I'=1πa2×πr2=Ir2a2
Applying Amphere's law,
BL=μ0I'
or B×2πr=μ0lr2a2
or B=(μ0I2πa2)r[Forr<a]
i.e., B∝r [For inside points ]
Thus, the field B is proportional to r as we move from the axis of the cylinder towards its surface and then it decreases as 1r. The variation of B with distance r from the centre of the wire is shown in figure.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
5 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-C
55 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
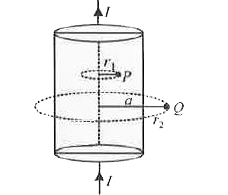
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
View Solution
Knowledge Check
A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A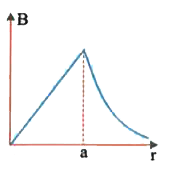 B
B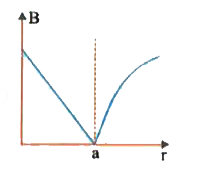 C
C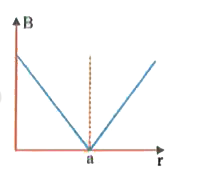 D
D
The figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
A2:1B1:2C4:1D1:1
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionA long straight wire of a circular cross section (radius a) carries a steady current 7 and the current / is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance from the centre of the wire?
View Solution
