A potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
To solve the problem step by step, we will follow the process of determining the emf of the primary cell using the given information about the potentiometer setup.
Step 1: Understand the Setup
We have a potentiometer wire of length 1 m and resistance 10 Ω connected in series with a 5 Ω resistor to a 6 V battery. The balance point is found at 40 cm (0.40 m).
Step 2: Calculate Total Resistance
The total resistance in the circuit can be calculated as follows:
- Resistance of the potentiometer wire = 10 Ω
- Resistance in series = 5 Ω
- Total resistance (R_total) = R_potentiometer + R_series = 10 Ω + 5 Ω = 15 Ω
Step 3: Calculate the Current in the Circuit
Using Ohm's law, we can find the current (I) flowing through the circuit:
I=VRtotal=6 V15 Ω=0.4 A
Step 4: Calculate the Voltage Across the Potentiometer
The voltage (V_pot) across the potentiometer wire can be calculated using Ohm's law:
Vpot=I×Rpotentiometer=0.4 A×10 Ω=4 V
Step 5: Calculate the Potential Gradient
The potential gradient (K) is the voltage per unit length of the potentiometer wire:
K=VpotL=4 V1 m=4 V/m
Step 6: Calculate the EMF of the Primary Cell
The emf (E) of the primary cell can be calculated using the formula:
E=K×Lbalance
Where Lbalance is the length at which the balance point is found (0.40 m):
E=4 V/m×0.40 m=1.6 V
Final Answer
The emf of the primary cell is 1.6 V.
---
We have a potentiometer wire of length 1 m and resistance 10 Ω connected in series with a 5 Ω resistor to a 6 V battery. The balance point is found at 40 cm (0.40 m).
The total resistance in the circuit can be calculated as follows:
- Resistance of the potentiometer wire = 10 Ω
- Resistance in series = 5 Ω
- Total resistance (R_total) = R_potentiometer + R_series = 10 Ω + 5 Ω = 15 Ω
Using Ohm's law, we can find the current (I) flowing through the circuit:
I=VRtotal=6 V15 Ω=0.4 A
The voltage (V_pot) across the potentiometer wire can be calculated using Ohm's law:
Vpot=I×Rpotentiometer=0.4 A×10 Ω=4 V
The potential gradient (K) is the voltage per unit length of the potentiometer wire:
K=VpotL=4 V1 m=4 V/m
The emf (E) of the primary cell can be calculated using the formula:
E=K×Lbalance
Where Lbalance is the length at which the balance point is found (0.40 m):
E=4 V/m×0.40 m=1.6 V
The emf of the primary cell is 1.6 V.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:[SET - II DELHI BOARD]
Explore 6 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:[SET - III, DELHI BOARD]
Explore 6 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET - III (Delhi Board)
Explore 8 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A potentiometer wire of length 1 m has a resistance of 10 Ω . It is connected to a 6 V battery in series with a resistance of 5 Ω . Determine the emf of the primary cell which gives a balance point at 40 cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 10Ω. It is connected to a 6 V battery in seried with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40 cm.
View Solution
Knowledge Check
A potentiometer wire has a length 2 m and resistance of 10Ω. It is coonnected in series with a resistance of 990Ω and a cell of e.m.f. 2 V. The potential gradient along the wire is
A0.01V/mB0.02V/mC0.03V/mD0.025V/m
A potentiometer wire of length 1 m has a resistance of 5Ω. It is connected to a 8 V battery in series with a resistance of 15Ω. Determine the emf of the primary cell which gives a balance point at 60 cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 100Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionA potentiometer wire of length 1m has a resistance 20Omega .It is connected in series with a resistance R and a cell of emf 2 volts.If potential gradient is 1V/m .Find R
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and of of 40cm of the potentiometer wire. What is the value of R?
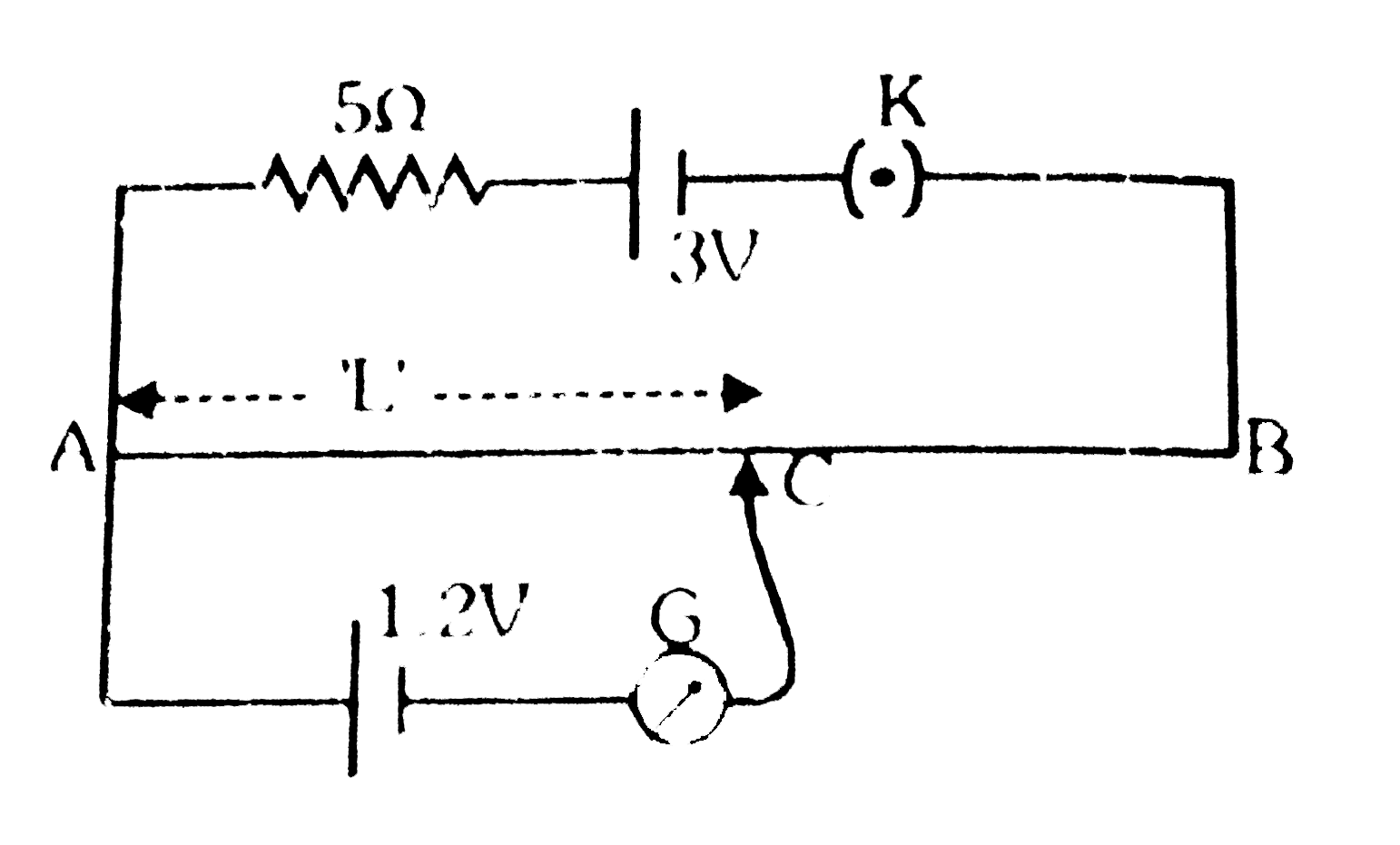
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
View Solution

