Show variation of resistivity of copper as a function of temperature in a graph.
To show the variation of resistivity of copper as a function of temperature, we can follow these steps:
Step 1: Understand the relationship between resistivity and temperature
Resistivity (ρ) of a conductor like copper increases with temperature. The relationship can be expressed as:
ρ(T)=ρ0(1+α(T−T0))
where:
- ρ(T) is the resistivity at temperature T,
- ρ0 is the resistivity at a reference temperature T0,
- α is the temperature coefficient of resistivity,
- T is the temperature in degrees Celsius.
Step 2: Choose a reference temperature
For copper, a common reference temperature is 20∘C (room temperature). At this temperature, the resistivity is approximately 1.68×10−8Ω⋅m.
Step 3: Calculate resistivity at different temperatures
Using the formula, we can calculate resistivity at various temperatures. For example:
- At 0∘C:
ρ(0)=ρ0(1+α(0−20))
- At 50∘C:
ρ(50)=ρ0(1+α(50−20))
- At 100∘C:
ρ(100)=ρ0(1+α(100−20))
- At 150∘C:
ρ(150)=ρ0(1+α(150−20))
Step 4: Plot the graph
1. X-axis: Temperature (°C)
2. Y-axis: Resistivity (Ω⋅m)
- Mark the calculated resistivity values at 0∘C,50∘C,100∘C, and 150∘C.
- Connect the points smoothly to show the parabolic nature of the graph.
Step 5: Analyze the graph
The graph will show an upward curve, indicating that as temperature increases, the resistivity of copper also increases. This relationship is typically parabolic due to the linear dependence of resistivity on temperature.
Final Graph
The final graph will have:
- A curve starting from the lower left (at lower temperatures) and rising as it moves to the right (higher temperatures).
- Specific points plotted at 0∘C,50∘C,100∘C, and 150∘C with corresponding resistivity values.
Resistivity (ρ) of a conductor like copper increases with temperature. The relationship can be expressed as:
ρ(T)=ρ0(1+α(T−T0))
where:
- ρ(T) is the resistivity at temperature T,
- ρ0 is the resistivity at a reference temperature T0,
- α is the temperature coefficient of resistivity,
- T is the temperature in degrees Celsius.
For copper, a common reference temperature is 20∘C (room temperature). At this temperature, the resistivity is approximately 1.68×10−8Ω⋅m.
Using the formula, we can calculate resistivity at various temperatures. For example:
- At 0∘C:
ρ(0)=ρ0(1+α(0−20))
- At 50∘C:
ρ(50)=ρ0(1+α(50−20))
- At 100∘C:
ρ(100)=ρ0(1+α(100−20))
- At 150∘C:
ρ(150)=ρ0(1+α(150−20))
1. X-axis: Temperature (°C)
2. Y-axis: Resistivity (Ω⋅m)
- Connect the points smoothly to show the parabolic nature of the graph.
The graph will show an upward curve, indicating that as temperature increases, the resistivity of copper also increases. This relationship is typically parabolic due to the linear dependence of resistivity on temperature.
The final graph will have:
- A curve starting from the lower left (at lower temperatures) and rising as it moves to the right (higher temperatures).
- Specific points plotted at 0∘C,50∘C,100∘C, and 150∘C with corresponding resistivity values.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:[SET - II DELHI BOARD]
Explore 6 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:[SET - III, DELHI BOARD]
Explore 6 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET - III (Delhi Board)
Explore 8 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
Knowledge Check
Which of the following graphs correctly shows variation of coefficient of volume expansion of copper as a function of temperature ?
A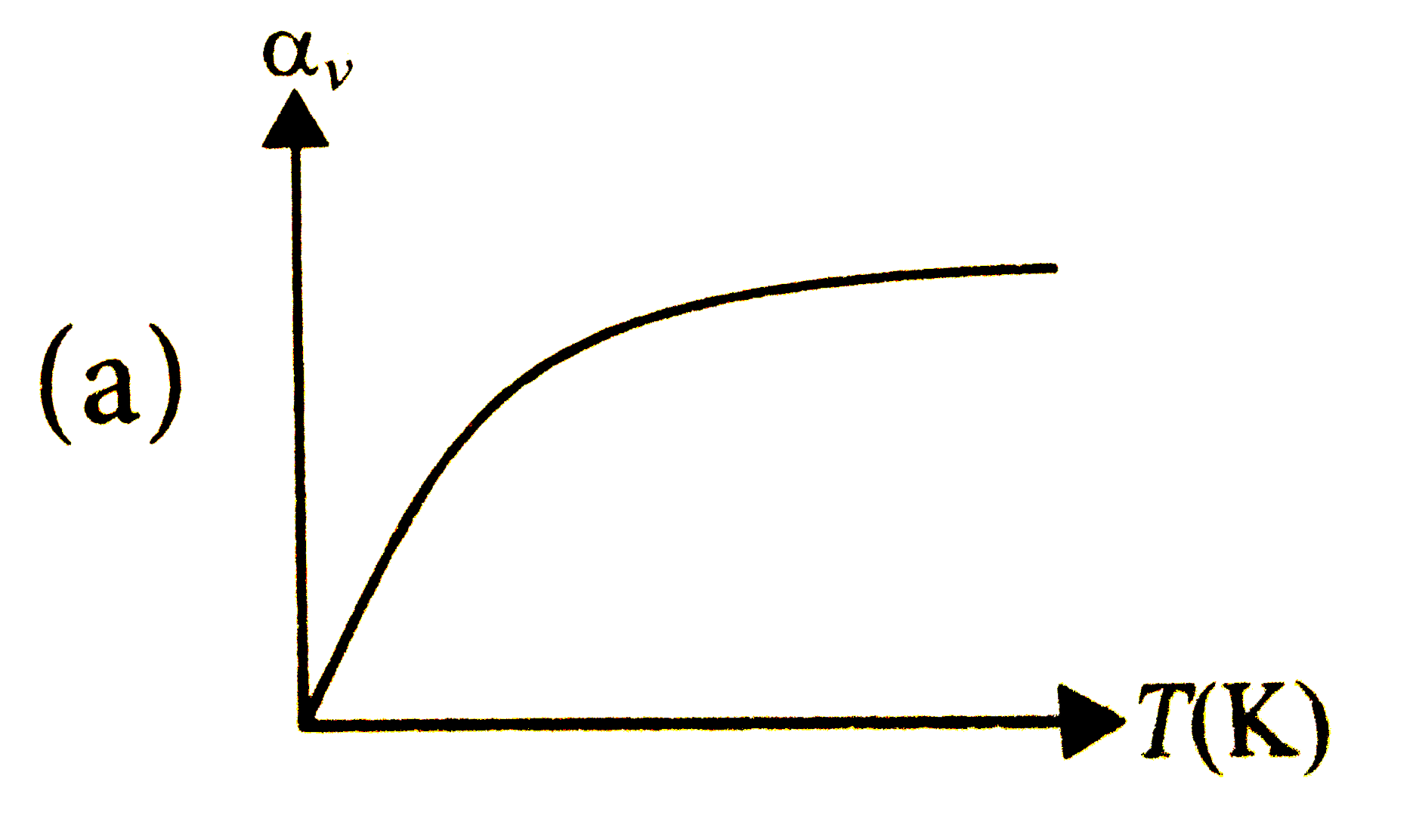 B
B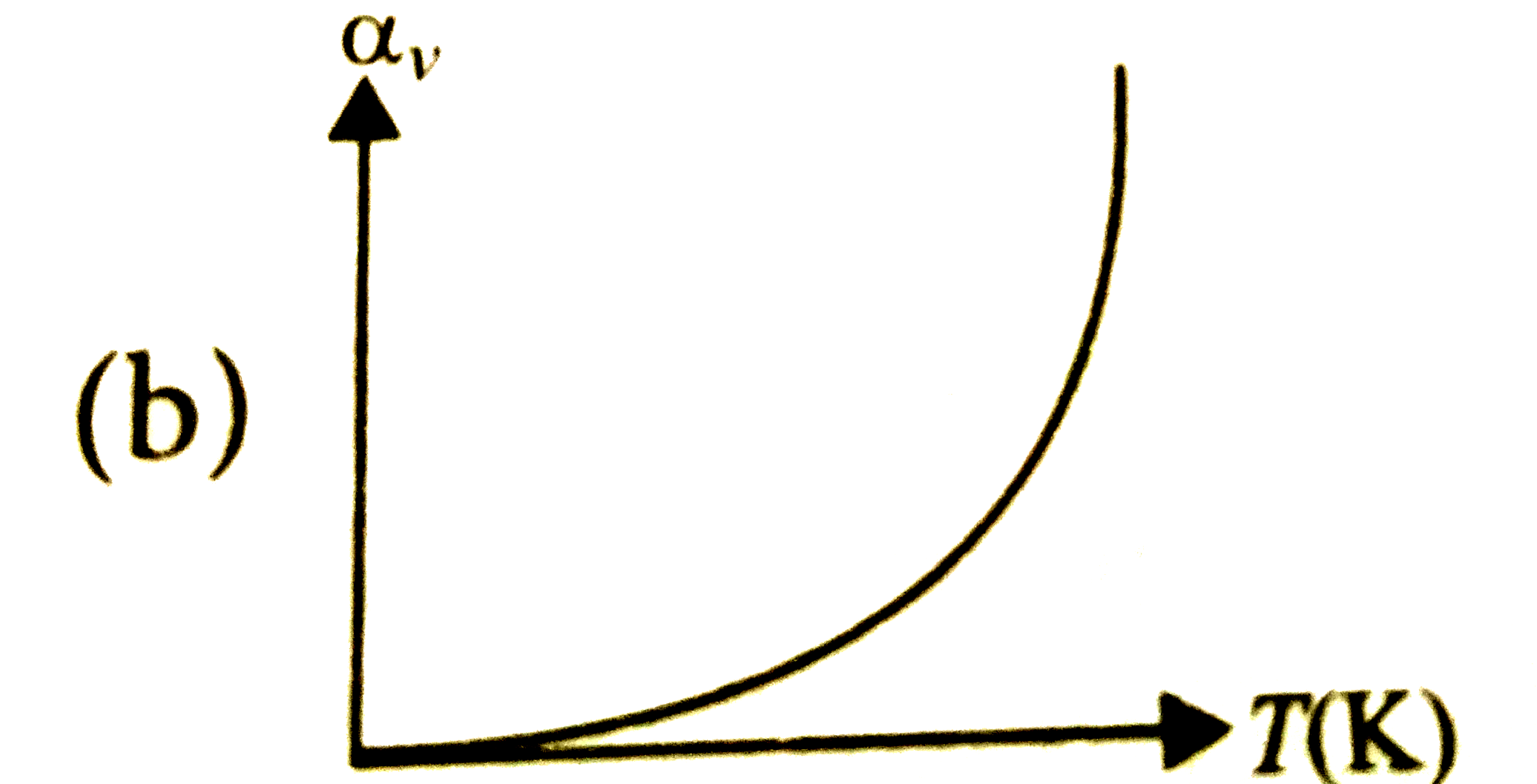 C
C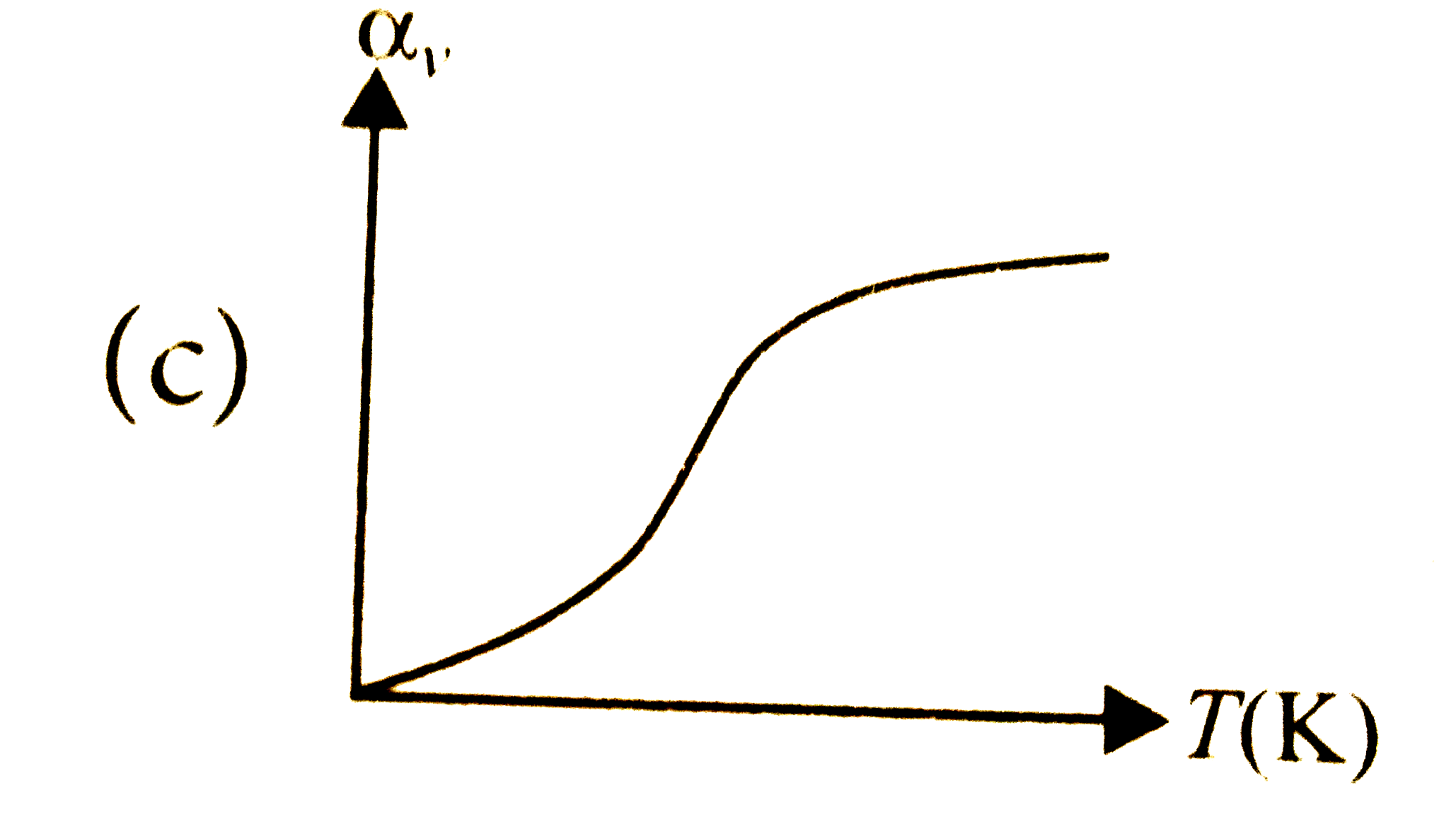 D
D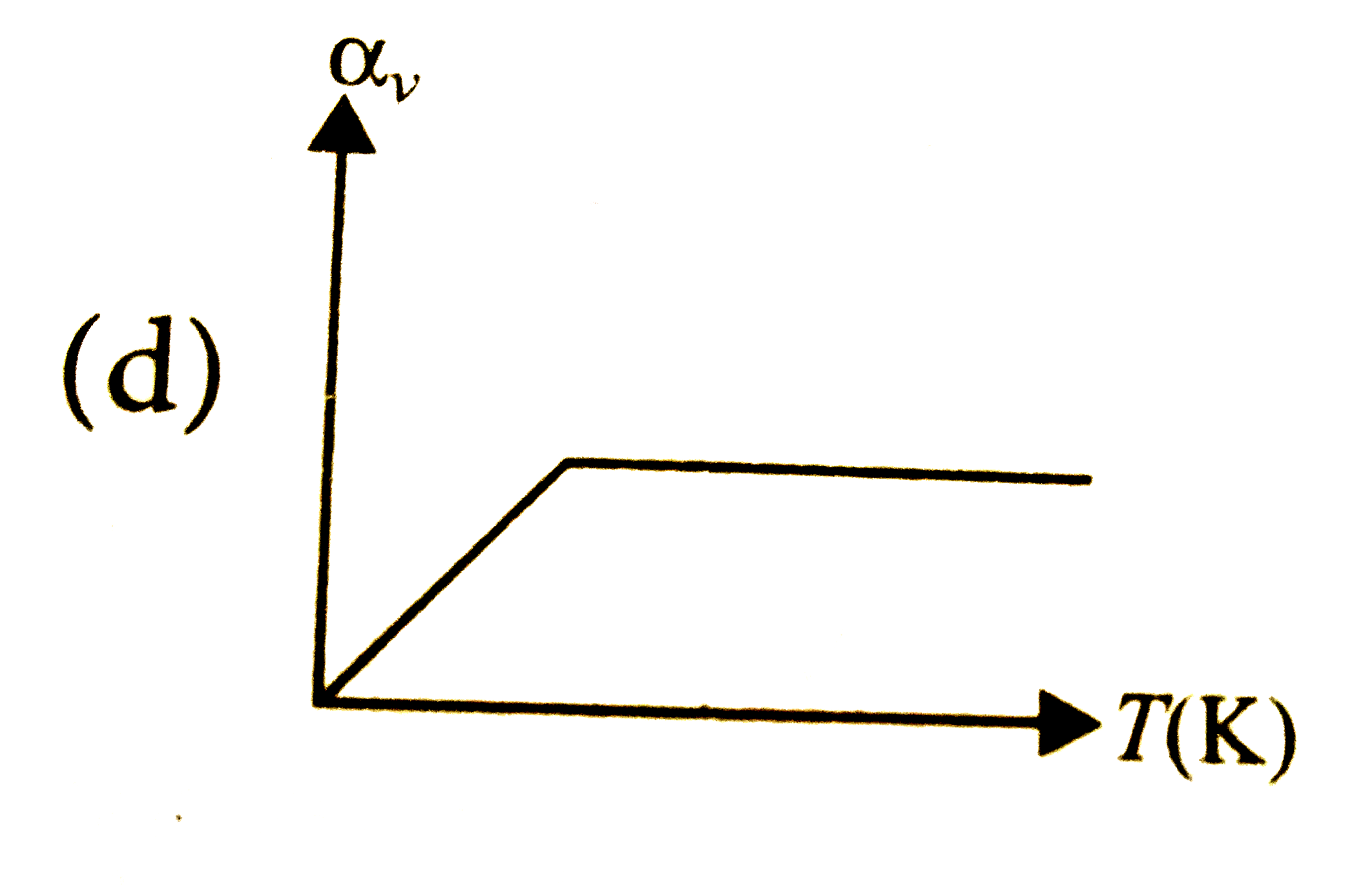
Draw a graph to show the variation of resistance of a metal wire as a function of its diameter, keeping length and temperature constant.
View SolutionDraw the graph showing variation of the value of the induced emf as a function of rate of change of current flowing through an ideal inductor.
View SolutionDraw the graph showing variation of the value of the induced emf as a function of rate of change of current flowing through an ideal inductor.
View SolutionSketch a graph showing variation of resistivity with temperature of (i) Copper (ii) Carbon.
View SolutionPlot a graph showing the variation of resistance of a conducting wire as function of its radius, keeping the length of a wire and its temperature as constant.
View SolutionThe variation of resistance of a metallic conductor with temperature is shown in figure. (i) Calculate the temperature coefficient of resistance from the graph. (ii) State why the resistance of the conductor increases with the rise in temperature.

View SolutionThe given graph shows the variation of resistance of mercury in the temperature range 0 lt T lt 4 K. Name the phenomeon shown by the graph.
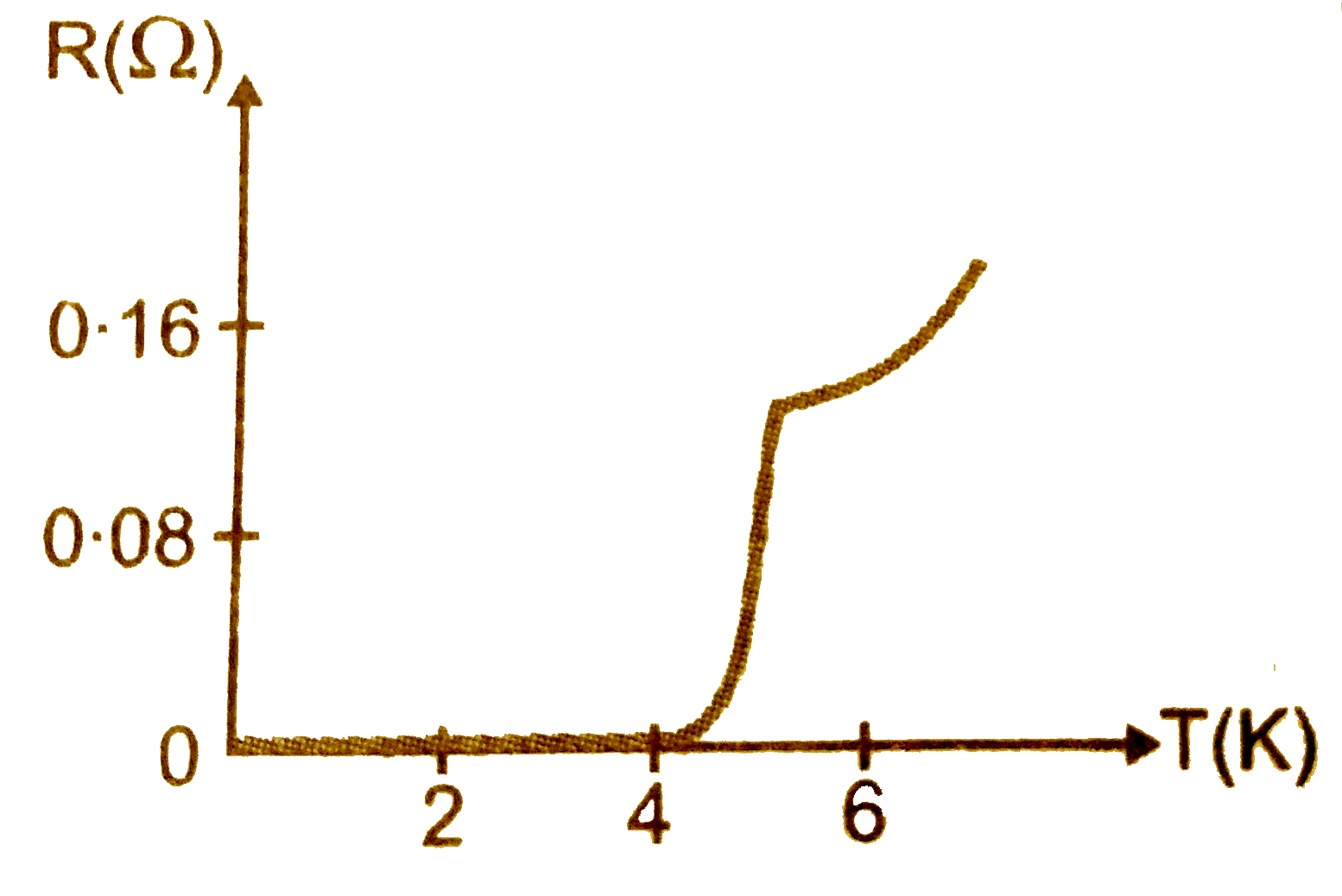
View Solution

