Conditions Of Total Internal Reflection
Essential conditions for total internal reflection:
(i) Light should travel from a denser medium to a rarer medium.
(ii) Angle of incidence in denser medium should be greater than the critical angle for the pair of media in contact.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-II
35 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III
25 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET III
9 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
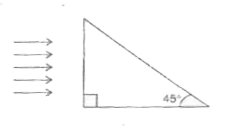
For a given incident ray as shown in Fig., the condition of total internal reflection of ray will be satisfied if the refractive index of the block will be.
 .A√3+12B√2+12C√32D√76
.A√3+12B√2+12C√32D√76Preferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q Now instead of changing the material of prism, we change one of the angle of prism to 300 Then, which of the colour gets separated?

 AredBgreenCblueDnone of these
AredBgreenCblueDnone of thesePreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q An experiment was performed based on the above theory with red, green and blue light. Their refractive indices in the material were 1.39, 1.44 and 1.47, respectively. Which colour would get separated?
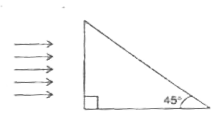 AredBgreenCblueDno colour would be separated.
AredBgreenCblueDno colour would be separated.
What is total internal reflection of light ? What are conditions for total internal reflection ?
View SolutionWhat is total internalreflection ? What is the meaning of critical angle ? What are the necessary conditions for total internal reflection ?
Write the relation between critical angle and refractive index of the medium.
View SolutionState the conditions of total internal reflection. Refractive indices of the given prism material for Red, Blue and Green colors are respectively 1.39, 1.48 and 1.42 respectively. Trace the path of rays through the prism.
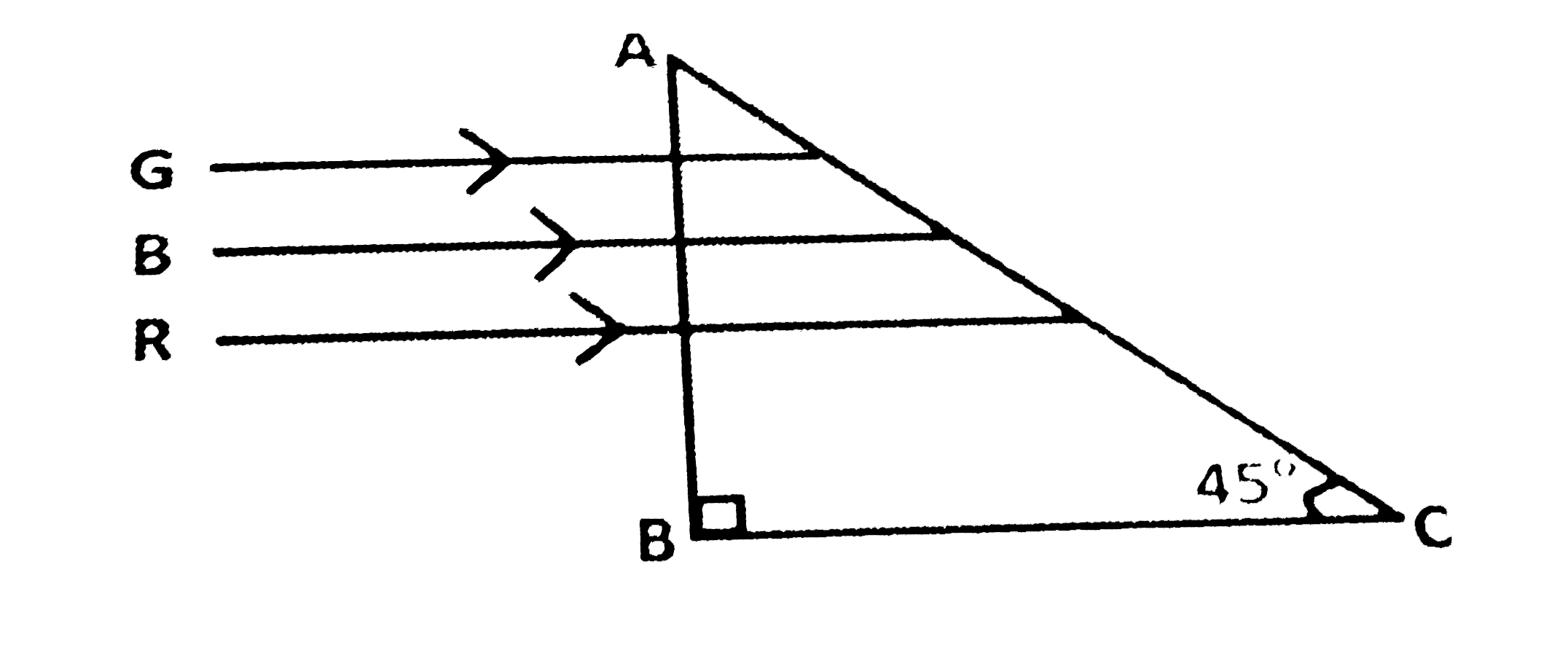
View SolutionState the conditions of total internal reflection. Refractive indices of the given prism material for Red, Blue and Green colours are respectively 1.39, 1.48 and 1.42 respectively. Trace the path of rays through the prism.
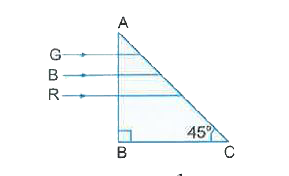
View SolutionPreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q As the density of the material-of the prism keeps on increasing, then which of the following statement holds good
View Solution
