Question

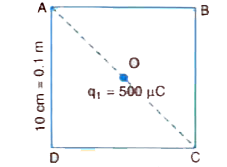
A 500 $\mu$ C charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10 $\mu$ C between two diagonally opposite points on the square.

Explanation

To solve the problem of finding the work done in moving a charge of 10 µC between two diagonally opposite points on a square with a 500 µC charge at the center, we can follow these steps:

Step 1: Understand the configuration
- We have a square of side 10 cm (0.1 m).
- A charge of 500 µC (which is 500 x 10^-6 C) is placed at the center of the square.
- We need to move a charge of 10 µC (10 x 10^-6 C) between two diagonally opposite corners of the square.

Step 2: Calculate the distance from the center to a corner
- The distance from the center of the square to any corner can be calculated using the Pythagorean theorem.
- The distance from the center to a corner (d) is given by:
\( d = \frac{\sqrt{(0.1)^2 + (0.1)^2}}{2} = \frac{\sqrt{0.01 + 0.01}}{2} = \frac{\sqrt{0.02}}{2} = \frac{0.1\sqrt{2}}{2} = \frac{0.1}{\sqrt{2}} \text{ m} \)

Step 3: Calculate the electric potential at the corners
- The electric potential (V) due to a point charge is given by:
\( V = \frac{k \cdot Q}{r} \)
where \(k\) is Coulomb's constant (\(8.99 \times 10^9 \, \text{N m}^2/\text{C}^2\)), \(Q\) is the charge at the center, and \(r\) is the distance from the charge to the point where we are calculating the potential.

- For both corners A and B:
\( V_A = V_B = \frac{k \cdot 500 \times 10^{-6}}{\frac{0.1}{\sqrt{2}}} \)

Step 4: Determine the work done in moving the charge
- The work done (W) in moving a charge in an electric field is given by:
\( W = Q \cdot (V_B - V_A) \)
- Since \(V_A = V_B\), we have:
\( W = 10 \times 10^{-6} \cdot (V_B - V_A) = 10 \times 10^{-6} \cdot 0 = 0 \)

Final Answer:
The work done in moving the charge of 10 µC between the two diagonally opposite points on the square is 0 Joules.