A charge of is placed at the centre of a spherical shell of radius 10cm. What will be the work done in moving a charge of on its surface through a distance of 5 cm?
To solve the problem, we need to determine the work done in moving a charge of +1 µC on the surface of a spherical shell with a radius of 10 cm, while a charge of +1 C is placed at the center.
1. Understanding the Setup:
- We have a charge of +1 C located at the center of a spherical shell with a radius of 10 cm.
- We need to move a charge of +1 µC (which is equal to 1×10−6 C) on the surface of this shell.
2. Electric Field Inside the Shell:
- According to Gauss's law, the electric field inside a conducting shell is zero. Therefore, the electric field at any point inside the shell (including at the surface) due to the charge at the center is zero.
3. Electric Potential on the Surface:
- The potential at the surface of the spherical shell is constant because it is an equipotential surface. The presence of the charge at the center creates a uniform electric potential across the surface of the shell.
4. Work Done in Moving the Charge:
- The work done W in moving a charge in an electric field is given by the formula:
W=q⋅(Vf−Vi)
where q is the charge being moved, Vf is the final potential, and Vi is the initial potential.
- Since the charge is being moved on the surface of an equipotential surface, the initial and final potentials are the same (Vf=Vi).
- Therefore, the work done in moving the charge is:
W=q⋅(V−V)=q⋅0=0
5. Conclusion:
- The work done in moving the charge of +1 µC on the surface of the spherical shell through a distance of 5 cm is 0 Joules.
- We have a charge of +1 C located at the center of a spherical shell with a radius of 10 cm.
- We need to move a charge of +1 µC (which is equal to 1×10−6 C) on the surface of this shell.
- According to Gauss's law, the electric field inside a conducting shell is zero. Therefore, the electric field at any point inside the shell (including at the surface) due to the charge at the center is zero.
- The potential at the surface of the spherical shell is constant because it is an equipotential surface. The presence of the charge at the center creates a uniform electric potential across the surface of the shell.
- The work done W in moving a charge in an electric field is given by the formula:
W=q⋅(Vf−Vi)
where q is the charge being moved, Vf is the final potential, and Vi is the initial potential.
- Since the charge is being moved on the surface of an equipotential surface, the initial and final potentials are the same (Vf=Vi).
- Therefore, the work done in moving the charge is:
W=q⋅(V−V)=q⋅0=0
- The work done in moving the charge of +1 µC on the surface of the spherical shell through a distance of 5 cm is 0 Joules.
Similar Questions
Knowledge Check
There is 10 units of charge at the centre of a circle of radius 10m. The work done in moving 1 unit of charge around the circle once is
AzeroB10 unitsC100 unitsD1 unitA charge of 5C is placed at the curve of a spherical gaussian of radius 5cm the electric flux through the surface is 1ε0 times of
A0.1N−m−2/CB0.5N−m2/CC1N−m2/CD5N−m2/CA ball with charge −50e is placed at the centre of a hollow spherical shell has a net charge of −50e. What is the charge on the shell's outer surface ?
A−50eBzeroC−100eD+100e
A charge q is placed at the centre of an imaginary spherical surface. What will be the electric flux due to this charge through any half of the sphere.
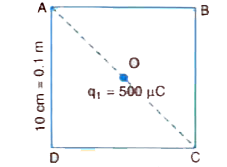
View SolutionA500μC charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10μC between two diagonally opposite points on the square.
View Solution" A change of "8.85C" is placed at the centre of a spherical Guassion surface of radius "5cm" .The electric flux through the surface "
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA charge 10μC is placed at the centre of a hemisphere of radius R=10cm as shown. The electric flux through the hemisphere (in MKS units)is

View Solution

