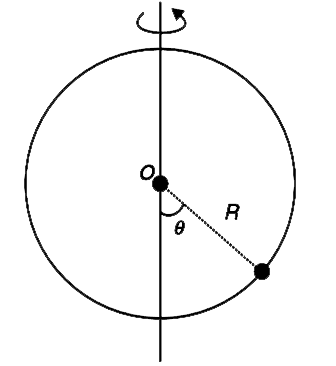
A thin circular loop of radius R rotates about its vertical diameter with an angular frequency co.
Show that a small bead on the wire remains at its lowermost point for ω≤√g/R . What is the angle made by the radius vector joining the centre to the bead with vertical downward direction for ω=√2g/R 1 Neglect friction.Solution in Gujrati
Consider the free-body diagram of the bead when the radius vector joining the centre of the wire makes an angle θ with the vertical downward direction. We have mg =Ncosθ and mRsinθω2=Nsinθ . These equations givecosθ=g/Rω2. Since cosθ≤1, the bead remains at its lowemost point ω≤√gR
For ω=√2gR,cosθ=12i.eθ=60∘
Topper's Solved these Questions
- BOOK - NCERT GUJARATICHAPTER - LAW OF MOTIONEXERCISE - EXERCISE23videos
LAW OF MOTION
- BOOK - NCERT GUJARATICHAPTER - KINETIC THEORYEXERCISE - ADDITIONAL EXERCISE4videos
KINETIC THEORY
- BOOK - NCERT GUJARATICHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE31videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
Give the magnitude and direction of the net force acting on (a) a drop of rain falling down with a constant speed, (b) a cork of mass 10 g floating on water, (c) a kite skillfully held stationary in the sky, (d) a car moving with a constant velocity of 30 km/h on a rough road, (e) a high-speed electron in space far from all material objects, and free of electric and magnetic fields.
03:42View SolutionA metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom ?
14:26View SolutionExplain why
The angle of contact of mercury with glass is obtuse. While that of water with glass is acute .04:41View SolutionA thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
05:08View SolutionA thin ring of radius R is made of a material of density rho and Young's modulus Y. If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increases in its radius.
05:39View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius (a sqrt(3))/(2) is :
04:59View SolutionA circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
 05:43View Solution
05:43View SolutionR त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है । यह दर्शाइए कि इस तार में डली कोई मणिका ω≤√g/R के लिए अपने निम्नतम बिंदु पर रहती है | ω=√2g/R के लिए, केंद्र से मणिका को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है ।
(घर्षण को उपेक्षणीय मानिए ।)View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire loop remains at its lowermost point for omegalesqrt(g//R) . What is the angle made by the radius vector joining the centre to bead with the vertical downward direction for omega=sqrt(2g//R) ? Neglect friction .
View SolutionA circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed omega . What is the value of angle theta , when the bead is in dynamic equilibrium ?
05:13View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω . Show that a small bead on the wire loop remains at its lowermost point for ω<√g/R What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? neglect friction.
View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire loop remains at its lowermost point for omega lt sqrt( g// R) What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for omega = sqrt(2g// R) ? neglect friction.
04:41View SolutionA thin circular wire of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire remain at its lowermost point for omegalesqrt(g//R) . What is angle made by the radius vector joining the center to the bead with the vertical downward direction for omega=sqrt(2g//R) ? Neglect friction.
06:39View SolutionA thin ring of radius R is made of material of density P and young.s modulus Y. If the ring is rotated about its centre and in its own plane with angular velocity ω find the small increase in its radius.
02:44View SolutionA thin circular wire of radius R rotates about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
05:04View SolutionA thin ring of radius R is made of a material of density rho and Young's modulus Y . If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increase in its radius.
05:26View Solution
