Find the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers. Solution in Gujrati
The correct Answer is:(i) -2 (ii) 2 (iii) −32(iv)32 (v) 0 (vi) 0 (vii) (-q)/(p)
Step by step video, text & image solution for Find the zero of the polynomial in each of the following cases. (i) f (x) = x +2 (ii) f (x) = x-2 (iii) f (x) =2x +3 (iv) f (x) =2x -3 (v) f (x) =x ^(2) (vi) f (x) = px, p ne 0 (vii) f (x) = px + q,p ne 0 pq are real numbers. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- POLYNOMIALS AND FACTORISATION BOOK - NCERT GUJARATICHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.3
9 Videos
- POLYNOMIALS AND FACTORISATION BOOK - NCERT GUJARATICHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.4
10 Videos
- POLYNOMIALS AND FACTORISATION BOOK - NCERT GUJARATICHAPTER - POLYNOMIALS AND FACTORISATION EXERCISE - EXERCISE 2.1
6 Videos
- LINES AND ANGLES BOOK - NCERT GUJARATICHAPTER - LINES AND ANGLES EXERCISE - THINK, DISCUSS AND WRITE
1 Videos
- PROBABILITY BOOK - NCERT GUJARATICHAPTER - PROBABILITY EXERCISE - DO THIS
3 Videos
Similar Questions
Find the remainder when x3+3x2+3x+1 is divided by the following Linear polynomials:
(i) x+1
(ii) x−12
(iii) x
(iv) x+π
(v) 5+2x
View SolutionDetermine which of the following polynomials has (x+1) as a factor.
(i) x3−x2−x+1
(ii) x4−x3+x2−x+1
(iii) x4+2x3+2x2+x+1
(iv) x3−x2−(3−√3)x+√3
View SolutionFind the degree of each of the polynomials given below
(i)x5−x4+3
(ii) x2+x−5
(iii) 5
(iv) 3x6+6y3−7
(v) 4−y2
(vi) 5t−√3
View SolutionWhat is the difference between intersecting lines and concurrent lines ?
View SolutionToss a coin for number of times as shown in the table. And record your findings in the table.

What happens if you keep on increasing the number of tosses.
View SolutionLet f(x) be a polynomial with real coefficients such that f(0)=1 and for all x ,f(x)f(2x^(2))=f(2x^(3)+x) The number of real roots of f(x) is:
View SolutionThe graph of y = f(x) is as shown in the following figure.
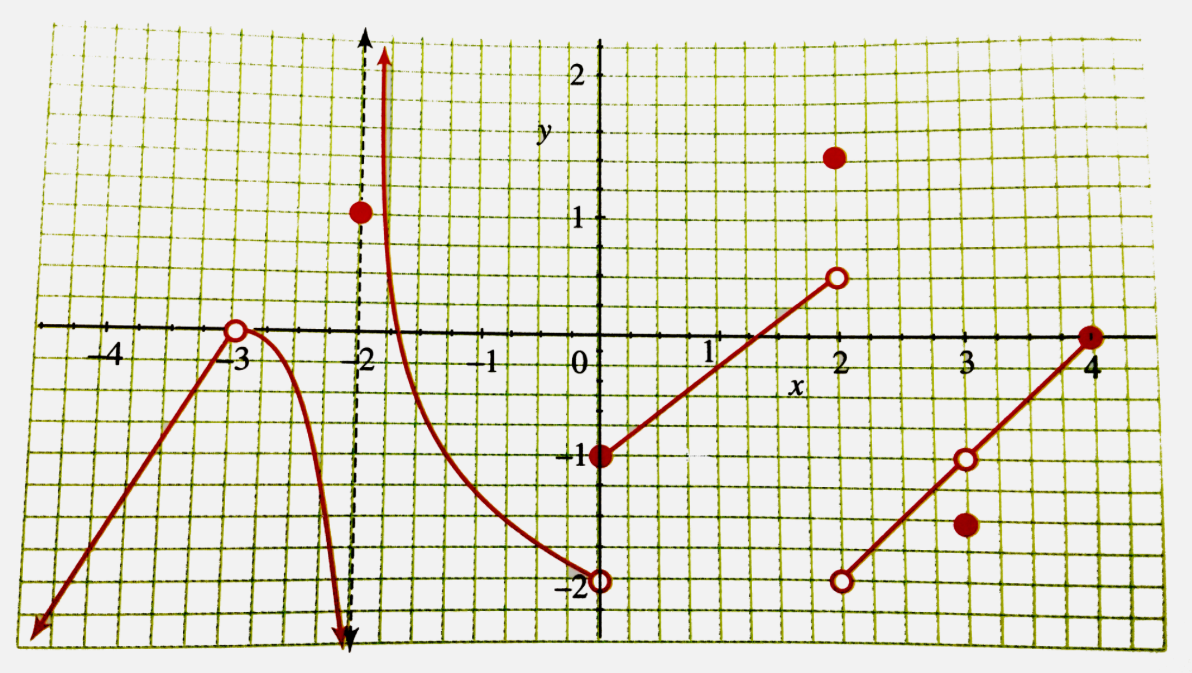
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f(x)=x3−2px2−4x+5 and f'(2)=0 find p .
View SolutionThe weakest acid HX ( X = F , Cl ,Br, I) is _________.
View SolutionLet f(x) = 2x + 5. If x ≠ 0 then find
f(x+2)−f(2)x
View SolutionThe order of reactivity of halogens is
(A) F>Cl>Br>I
(B) F < Cl < Br < I
(C) F < Cl > Br < I
(D) F < Cl < Br> I
View SolutionFind the zeros of the polynomial in each of the following.
(i) p(x)=x−3
(ii) p(x)=2x+5
(iii) q(y)=2y−3
(iv) f(z)=8z
( v) p(x)=axwhen a ≠ 0
(vi) h( x) =ax + b , a ne 0, a, b in R
View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.
View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.
View SolutionFind the zero of the polynomial in each of the following cases.
(i) f(x)=x+2
(ii) f(x)=x−2
(iii) f(x)=2x+3
(iv) f(x)=2x−3
(v)f(x)=x2
(vi) f(x)=px,p≠0
(vii) f(x)=px+q,p≠0pq are real numbers.
View Solution
