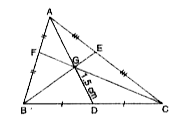
In a ΔABC, the medians AD, BE and CF passes through G. If FG = 3.5 cm. find GC.
6 cm
7 cm
8 cm
9 cm
The correct Answer is:B
To solve the problem, we need to find the length of segment GC in triangle ABC, where G is the centroid and FG is given as 3.5 cm.
1. Understanding the Centroid:
The centroid (G) of a triangle divides each median in the ratio of 2:1. This means that the segment from the vertex to the centroid (e.g., AG) is twice the length of the segment from the centroid to the midpoint of the opposite side (e.g., GC).
2. Identifying the Segments:
In this case, FG is given as 3.5 cm. Since FG is the segment from the centroid G to point F (which is on the median CF), we can denote:
- FG = 3.5 cm (this is the shorter segment)
- GC = ? (this is the longer segment we want to find)
3. Using the Ratio:
Since G divides the median in the ratio of 2:1, we can say that:
- FG : GC = 1 : 2
4. Setting Up the Equation:
Let GC = x. According to the ratio, we can express the relationship as:
- FG = 3.5 cm (1 part)
- GC = 2 parts = 2 * FG
5. Calculating GC:
Now, we can substitute FG into the equation:
- GC = 2 * 3.5 cm
- GC = 7 cm
6. Conclusion:
Therefore, the length of segment GC is 7 cm.
Final Answer:
GC = 7 cm
---
The centroid (G) of a triangle divides each median in the ratio of 2:1. This means that the segment from the vertex to the centroid (e.g., AG) is twice the length of the segment from the centroid to the midpoint of the opposite side (e.g., GC).
In this case, FG is given as 3.5 cm. Since FG is the segment from the centroid G to point F (which is on the median CF), we can denote:
- FG = 3.5 cm (this is the shorter segment)
- GC = ? (this is the longer segment we want to find)
Since G divides the median in the ratio of 2:1, we can say that:
- FG : GC = 1 : 2
Let GC = x. According to the ratio, we can express the relationship as:
- FG = 3.5 cm (1 part)
- GC = 2 parts = 2 * FG
Now, we can substitute FG into the equation:
- GC = 2 * 3.5 cm
- GC = 7 cm
Therefore, the length of segment GC is 7 cm.
GC = 7 cm
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, the median AD, BE and CF at G. then which of the following is correct?
AAD+BE+CF>12(AB+BC+AC)B2(AD+BE+CF)>(AB+BC+AC)C3(AD+BE+CF)>4(AB+BC+AC)DAB+BC+AC>AD+BE+CF - Question 2 - Select One
In an equilateral ΔABC, the medians AD, BE and CF interest to each other at point G. If the area of quadrilateral BDGF is 12√3cm3, then the side of ΔABC is:
AA)10√3 cmBB)10 cmCC)12√3 cmDD)12 cm - Question 3 - Select One
If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB=19 cm and AC=22cm then the length of BC is
A20.5 cmB19.5 cmC13 cmD25 cm
In ΔABC, the median AD is 7 cm and CB is 14 cm, measure of ∠CABis
View SolutionIn ΔABC medians BE and CF intersect at G. If the straight line AGD meets BC in D in such a way that GD = 1.5 cm, then the length of AD is :
 View Solution
View SolutionIn ΔABC, the medians AD and BE meet at G. The ratio of the areas of ΔBDG and the quadrilateral GDCE is :
View SolutionG is the centroid of ΔABC. The medians AD and BE Intersect at right angles. If the lengths of AD and BE are 9 cm and 12 cm re spectively, then the length of AB (in cm) is
View SolutionIn ΔABCtwo medians BE and CF intersect at the point O and P, Q are the midpoints of BO and CO respectively. If the length of PQ = 3cm, then the length of FE will be
View Solution
