Question

Derive the relation $f=R/2$ in the case of a concave mirror.

Explanation

To Show that `f = R //2` for a Concave Mirror .
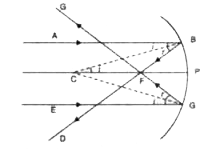
Let a ray of light AB be incident, parallel to the principal axis, on a concave mirror. After refraction, the ray AB passes along BD,through the focus F. BC is normal to the concave mirror at B.
`/_ABC = /_ CBD ` .....(1)
( According to the law of reflection ` /_i = /_ r )`
We know that AB and PC are parallel to each other.
`:. /_ ABC = /_ BCP ` ( alternate angles ) ....... (2)
From equations (1) and (2) , we get
`/_ CBD = /- BCP `
Hence triangle BCF is isosceles
`:. BF = CF` ....(3)
If the aperture of the mirror is small than B will be very close to P.
`:.` BF = PF ....(4)
From equation ( 3) and( 4) we conclude that
`CF = PF = ( 1)/(2) PC `
But by definition PF = f ( focal length ) and PC = R ( radius of curvature )
i.e., `f = ( R )/( 2)`