The uniform solid block in Fig. 10-62 has mass 0.172 kg and edge lengths a = 3.5 cm, b = 8.4 cm, and c = 1.4 cm. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces.
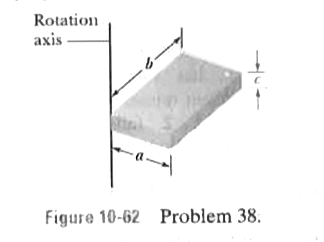
4.7×10−4kg⋅m2
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
43 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
The uniform solid block shown in figure has mass M and edge dimensions a, b, and c. Calculate its rotational inertia about an axis passing through one corner and perpendicular to the large faces.
View SolutionA solid cylinder of uniform density of radius 2 cm has mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
View Solution
Knowledge Check
A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A0.16 kg - m2B0.12 kg - m2C0.32 kg - m2D0.08 kg - m2A circular thin disc of mass 2 kg has a diameter 0.2 m. Calculate its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc (in kg m2)
A0.01B0.03C0.02D3Figure shows a uniform solid block of mass M and edge lengths a,b and c. Its M.I. about an axis through one edge and perpendicular (as shown) to the large face of the block is
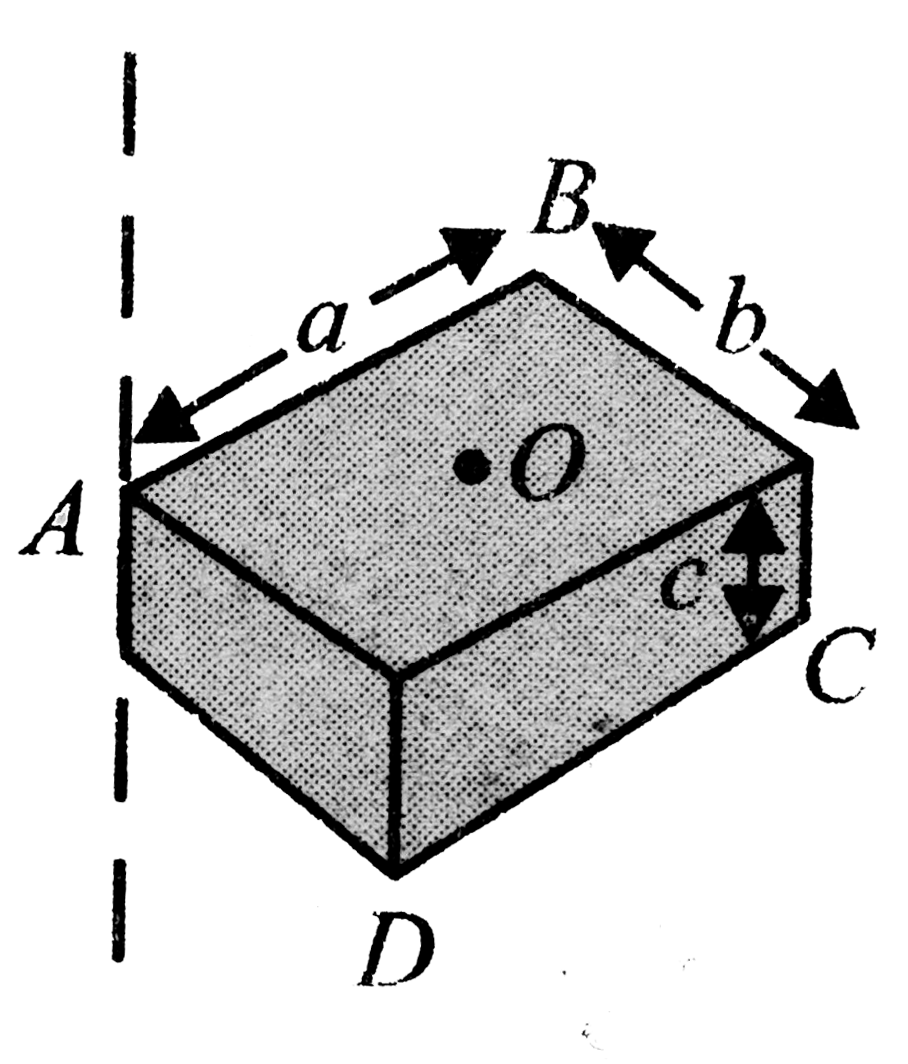 AM3(a2+b2)BM4(a2+b2)C7M12(a2+b2)DM12(a2+b2)
AM3(a2+b2)BM4(a2+b2)C7M12(a2+b2)DM12(a2+b2)
A 1m long rod has a mass of 0.12 kg. The moment of inertia about an axis passin through the centre and perpendicular to the length of rod will be
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionA uniform disc of mass 5 kg has a radius of 0.5 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is
View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
View Solution
