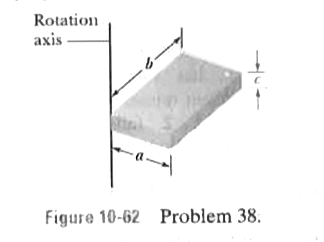
The uniform solid block shown in figure has mass M and edge dimensions a, b, and c. Calculate its rotational inertia about an axis passing through one corner and perpendicular to the large faces.
To calculate the rotational inertia (moment of inertia) of a uniform solid block about an axis passing through one corner and perpendicular to the large faces, we can follow these steps:
Step 1: Identify the dimensions and mass of the block
The block has mass M and edge dimensions a, b, and c. We need to find the moment of inertia about an axis that passes through one corner of the block and is perpendicular to the large faces.
Step 2: Understand the axis of rotation
The axis of rotation is perpendicular to the plane formed by the dimensions a and b. This means we can treat the block as a rectangular plate of dimensions a and b with thickness c.
Step 3: Moment of inertia of the rectangular plate about its center
For a rectangular plate of mass M with dimensions a and b, the moment of inertia about an axis perpendicular to its plane and passing through its center is given by:
Iz=M12(a2+b2)
Step 4: Apply the Parallel Axis Theorem
Since we need the moment of inertia about an axis that is not through the center but through one corner of the block, we can use the Parallel Axis Theorem. The theorem states:
Ix=Iz+Md2
where d is the distance from the center of mass axis to the new axis.
Step 5: Calculate the distance d
The distance d from the center of the rectangular plate to the corner (where the new axis is) can be calculated as:
d=12√a2+b2
This is because the center of mass is at (a2,b2) from the corner.
Step 6: Substitute values into the Parallel Axis Theorem
Now substituting Iz and d into the equation:
Ix=M12(a2+b2)+M(12√a2+b2)2
Calculating d2:
d2=(12√a2+b2)2=14(a2+b2)
Now substituting this back:
Ix=M12(a2+b2)+M⋅14(a2+b2)
Step 7: Combine terms
Combining the terms gives:
Ix=M12(a2+b2)+3M12(a2+b2)=4M12(a2+b2)=M3(a2+b2)
Final Answer
The rotational inertia of the solid block about the specified axis is:
Ix=M3(a2+b2)
The block has mass M and edge dimensions a, b, and c. We need to find the moment of inertia about an axis that passes through one corner of the block and is perpendicular to the large faces.
The axis of rotation is perpendicular to the plane formed by the dimensions a and b. This means we can treat the block as a rectangular plate of dimensions a and b with thickness c.
For a rectangular plate of mass M with dimensions a and b, the moment of inertia about an axis perpendicular to its plane and passing through its center is given by:
Iz=M12(a2+b2)
Since we need the moment of inertia about an axis that is not through the center but through one corner of the block, we can use the Parallel Axis Theorem. The theorem states:
Ix=Iz+Md2
where d is the distance from the center of mass axis to the new axis.
The distance d from the center of the rectangular plate to the corner (where the new axis is) can be calculated as:
d=12√a2+b2
This is because the center of mass is at (a2,b2) from the corner.
Now substituting Iz and d into the equation:
Ix=M12(a2+b2)+M(12√a2+b2)2
Calculating d2:
d2=(12√a2+b2)2=14(a2+b2)
Now substituting this back:
Ix=M12(a2+b2)+M⋅14(a2+b2)
Combining the terms gives:
Ix=M12(a2+b2)+3M12(a2+b2)=4M12(a2+b2)=M3(a2+b2)
The rotational inertia of the solid block about the specified axis is:
Ix=M3(a2+b2)
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
The uniform solid block in Fig. 10-62 has mass 0.172 kg and edge lengths a = 3.5 cm, b = 8.4 cm, and c = 1.4 cm. Calculate its rotational inertia about an axis through one corner and perpendicular to the large faces.
View SolutionA solid cylinder of uniform density of radius 2 cm has mass of 50 g. If its length is 12 cm, calculate its moment of inertia about an axis passing through its centre and perpendicular to its length.
View Solution
Knowledge Check
A circular thin disc of mass 2 kg has a diameter 0.2 m. Calculate its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc (in kg m2)
A0.01B0.03C0.02D3A solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
A2MR23+MI212BMR23+MI212C3MR23+MI212DMR24+MI212A solid cylinder has mass M radius R and length / its moment of inertia about an axis passing through its centre and perpendicular to its own axis is
A2MR23+MI212BMR23+MI212C3MR23+MI212DMR24+MI212
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
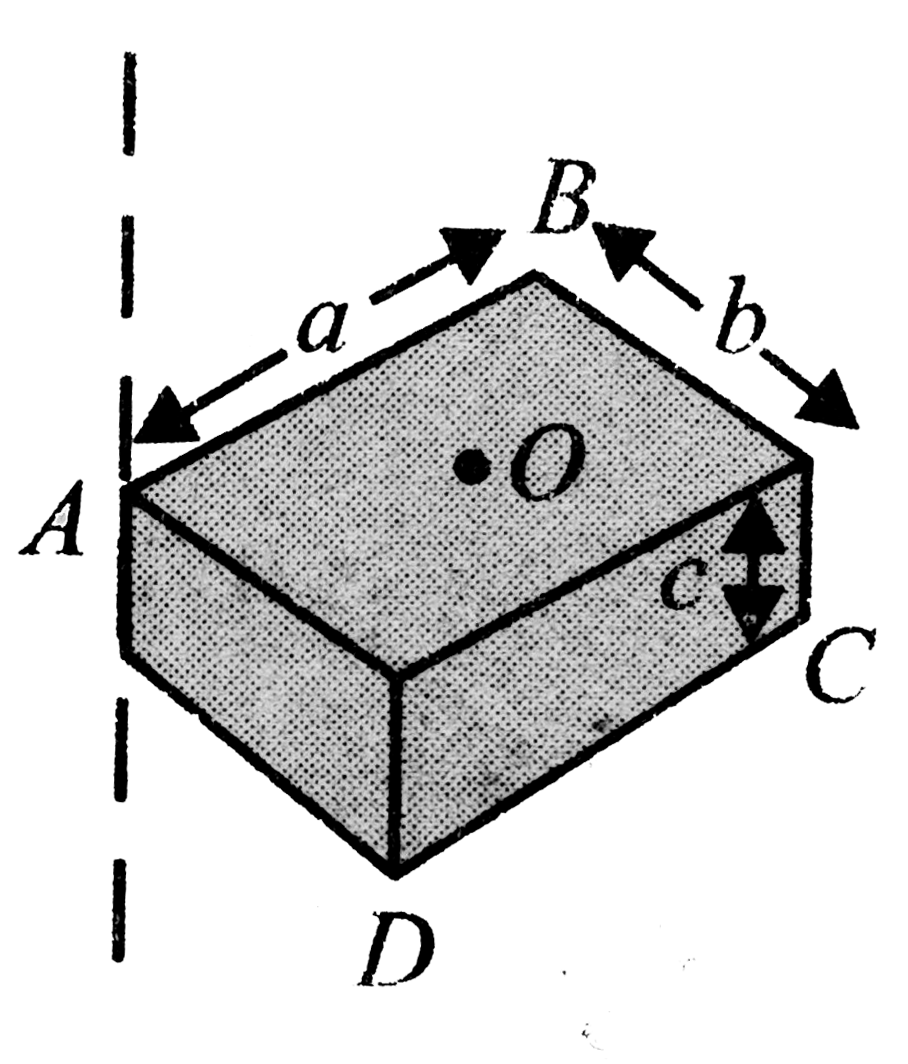
View SolutionFigure shows a uniform solid block of mass M and edge lengths a,b and c. Its M.I. about an axis through one edge and perpendicular (as shown) to the large face of the block is
View SolutionA uniform disc of mass 5 kg has a radius of 0.5 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is
View Solution
